Listes et fonctions¶
Graphique de fonctions¶
Dans cet échauffement, nous allons calculer les images d'une fonction pour tracer sa représentation graphique.
Recopier le programme suivant.
Modifier la ligne avec le print pour faire apparaitre l'image et l'antécédent à chaque ligne.
Commenter chaque ligne avec une attention particulière à la ligne qui commence par for...
from math import cos, pi
def f(x):
return cos(x*pi/2)
for x in range(40):
print(f(x))
Pour tracer le graphique de cette fonction, il faudrait enregistrer toutes ces valeurs et donc utiliser des variables.
Mettre plusieurs valeurs dans une seule variable c'est possible, on utilise des listes (on les a déjà rencontré plusieurs fois).
Recopier ce programme, commenter ce programme et retrouver où les listes apparaissent.
from math import cos, pi
def f(x):
return cos(x*pi/2)
images = []
antecedants = []
for x in range(20):
images.append(f(x))
print("Les images sont ", images)
Modifier votre programme pour enregistrer aussi les antecedants et les afficher à la fin
Nous allons maintenant enfin pouvoir tracer le graphique.
Ajouter la ligne suivante au début de votre programme.
import matplotlib.pyplot as plt
Ajouter cette ligne à la fin.
plt.plot(antecedants, images)
plt.show()
Vous avez tracer la courbe représentative de de la fonction $f$.
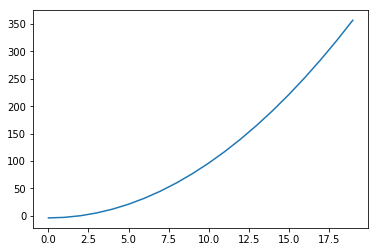
Dans un nouveau fichier, tracer la courbe représentative de la fonction $g$ tel que $$ g : x \mapsto x^2 - 4$$
Précision et controle du tracé¶
Pour le moment, on sait donner un maximum à l'antécédent $x$ mais on ne peut pas contrôler le minimum ni le pas (l'écart en 2 valeurs de $x$). Or pour tracer précisément la représentation graphique d'une fonction, nous avons besoin de contrôler la fenêtre (minimum et maximum) et le pas.
Boucle while (tant que )¶
Ce type de boucle donne plus de contrôle sur $x$ et nous évite d'utiliser range qui est une commande qui n'existe que en Python.
Les 2 programmes ci-dessous font la même chose.
for x in range(10):
print(x)
x = 0
while x < 10:
print(x)
x = x + 1
Commenter le programme avec le while.
Que se passe-t-il si on inverse les 2 dernières lignes?
Réécrire le programme suivant en utilisant une boucle while et en stockant les antécédents.
from math import sin, pi
def h(x):
return sin(x*pi/2)
images = []
antecedants = []
for x in range(20):
images.append(h(x))
antecedants.append(x)
print("Les images sont ", images)
Modifier votre programme pour que les antécédents aillent de -2 à 2.
Modifier votre programme pour que les antécédents augmentent avec un pas de 0.5 au lieu de 1.
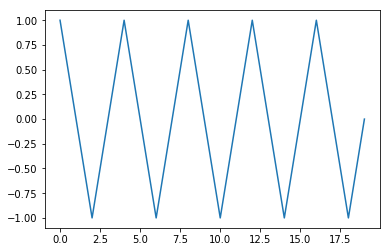
Tracer sa représentation graphique pour $x$ allant de -2 à 2 avec un pas de 1.
Tracer sa représentation graphique pour $x$ allant de -2 à 2 avec un pas de 0.5.
Tracer sa représentation graphique pour $x$ allant de -2 à 2 avec un pas de 0.1.
En regroupant les 3 programmes écrit précedement, tracer sur le même graphique les 3 représentations pour observer l'amélioration de la précision.
Astuce: pour tracer 3 graphiques en 1, on fait les plt.plot(...) de chaque graphique et uniquement à la fin on lance plt.show().