2018-04-10 11:22:39 +00:00
{
"cells": [
2018-04-12 18:06:58 +00:00
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Analyse des notes du DNB"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
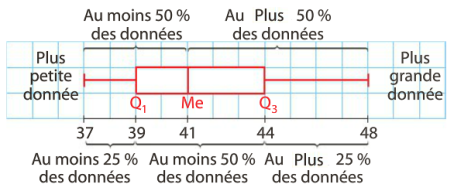
"En **bon** prof de math, on commence par un petit cours sur les boites à moustaches! C'est un **super** outils pour visualiser la répartition des données entre elles.\n",
"\n",
"On sépare les données en 4 groupes de même taille (25%). Un groupe dans une moustache, un dans une partie du corps, un dans l'autre partie du corps et le dernier dans l'autre moustache.\n",
"\n",
"\n",
"\n",
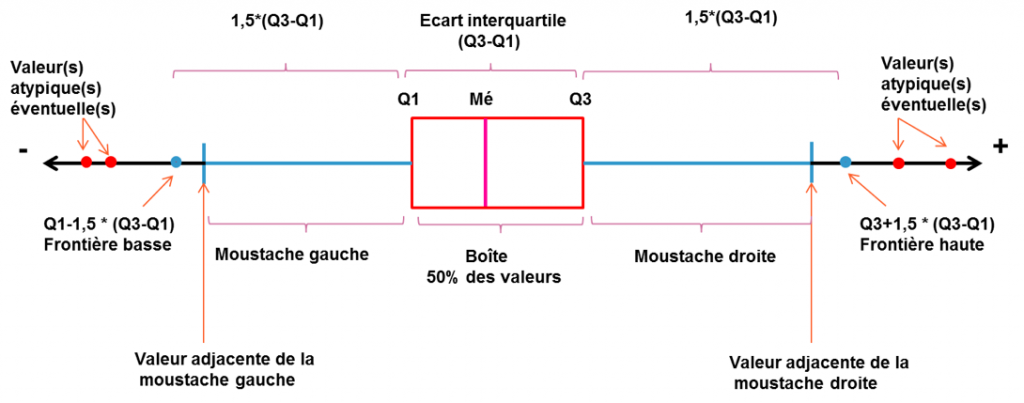
"Je laisse ceux qui ne sont pas partis en courant à appuyer sur la *flèche du bas* ou *espace* pour avoir une boite à moustache un peu plus complexe et complete.\n",
"\n",
"Pour les autres c'est *flèche de gauche*."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
""
]
},
2018-04-10 11:22:39 +00:00
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
2018-04-12 18:06:58 +00:00
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
2018-04-10 11:22:39 +00:00
},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"from math import ceil\n",
"import seaborn as sns\n",
"import matplotlib.pyplot as plt\n",
"%matplotlib inline\n",
"from pprint import pprint"
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 2,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [],
"source": [
"gene = [str(i) for i in range(301, 305)] + [str(i) for i in range(309, 312)]\n",
"pro = [str(i) for i in range(305, 309)] + [\"312\"]\n",
"coeff = {\n",
" \"Français\": 100,\n",
" \"HG\": 50,\n",
" \"Maths\": 100,\n",
" \"SVT\": 25,\n",
" \"Physique\": 25,\n",
" \"Techno\": 25\n",
"}\n",
"matieres = list(coeff.keys())\n",
"norm_matieres = [\"_\"+m for m in matieres]"
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 3,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"def orderedDict2df(sheets):\n",
" dfs = []\n",
" for tribe, df in sheets.items():\n",
" df['classe'] = tribe\n",
" dfs.append(df)\n",
" return pd.concat(dfs)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# DNB Général\n",
"\n",
"\n",
"Ici juqu'au contraire, on ne parlera que des classes qui ont passé le DNB générale."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"['301', '302', '303', '304', '309', '310', '311']"
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"gene"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [],
"source": [
"sheets_gene = pd.read_excel(\"./DNB blanc 1.xls\",\n",
" sheetname=gene,\n",
" skiprows=[0],\n",
" parse_cols=\"B,C,E,G,I,K,M\",\n",
2018-04-12 18:06:58 +00:00
" )\n"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 6,
2018-04-10 11:22:39 +00:00
"metadata": {
2018-04-12 18:06:58 +00:00
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
2018-04-10 11:22:39 +00:00
},
"outputs": [],
"source": [
2018-04-12 18:06:58 +00:00
"df = orderedDict2df(sheets_gene)"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 7,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [],
"source": [
2018-04-12 18:06:58 +00:00
"#df.head()"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 8,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df.columns = [\"Nom\", \"Français\", \"HG\", \"Maths\", \"SVT\", \"Physique\", \"Techno\", \"Classe\"]\n"
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"for m, coef in coeff.items():\n",
" df[m] = pd.to_numeric(df[m], errors='coerce')\n",
" df[\"_\"+m] = df[m]/coef\n",
"#df.head()"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df = df = df.assign(\n",
" total = df[matieres].sum(1),\n",
" maximum = 325\n",
")\n",
"df = df.assign(\n",
" normalisee = df[\"total\"]/df[\"maximum\"]\n",
")"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Les absents ont toujours tord. On les sort de toute l'analyse qui suiva.\n"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
2018-04-12 18:06:58 +00:00
" <th>Classe</th>\n",
" <th>Nom</th>\n",
" <th>Français</th>\n",
" <th>HG</th>\n",
" <th>Maths</th>\n",
" <th>SVT</th>\n",
" <th>Physique</th>\n",
" <th>Techno</th>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>20</th>\n",
" <td>302</td>\n",
" <td>INOUSSA Anchoura</td>\n",
" <td>36.5</td>\n",
" <td>12.0</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>6</th>\n",
" <td>303</td>\n",
" <td>ATTOUMANI Amin</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>9</th>\n",
" <td>304</td>\n",
" <td>M'MADI Abdourahim</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>26</th>\n",
" <td>309</td>\n",
" <td>YOUSSOUFA Elina (ULIS)</td>\n",
" <td>NaN</td>\n",
" <td>9.0</td>\n",
" <td>19.0</td>\n",
" <td>8.0</td>\n",
" <td>4.5</td>\n",
2018-04-10 11:22:39 +00:00
" <td>15.5</td>\n",
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>6</th>\n",
" <td>310</td>\n",
" <td>BACAR Abdallah</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>310</td>\n",
" <td>CHARKANE Farsa</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>311</td>\n",
" <td>ASSANE Kassim</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>8</th>\n",
" <td>311</td>\n",
" <td>BEN SOIGHIR Soirianti</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>9</th>\n",
" <td>311</td>\n",
" <td>BEN SOIGHIS AHAMADA Soirianti</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>12</th>\n",
" <td>311</td>\n",
" <td>DJAANFARI Haïria</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
2018-04-12 18:06:58 +00:00
" Classe Nom Français HG Maths SVT \\\n",
"20 302 INOUSSA Anchoura 36.5 12.0 NaN NaN \n",
"6 303 ATTOUMANI Amin NaN NaN NaN NaN \n",
"9 304 M'MADI Abdourahim NaN NaN NaN NaN \n",
"26 309 YOUSSOUFA Elina (ULIS) NaN 9.0 19.0 8.0 \n",
"6 310 BACAR Abdallah NaN NaN NaN NaN \n",
"9 310 CHARKANE Farsa NaN NaN NaN NaN \n",
"5 311 ASSANE Kassim NaN NaN NaN NaN \n",
"8 311 BEN SOIGHIR Soirianti NaN NaN NaN NaN \n",
"9 311 BEN SOIGHIS AHAMADA Soirianti NaN NaN NaN NaN \n",
"12 311 DJAANFARI Haïria NaN NaN NaN NaN \n",
2018-04-10 11:22:39 +00:00
"\n",
2018-04-12 18:06:58 +00:00
" Physique Techno \n",
"20 NaN NaN \n",
"6 NaN NaN \n",
"9 NaN NaN \n",
"26 4.5 15.5 \n",
"6 NaN NaN \n",
"9 NaN NaN \n",
"5 NaN NaN \n",
"8 NaN NaN \n",
"9 NaN NaN \n",
"12 NaN NaN "
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 11,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
2018-04-12 18:06:58 +00:00
"absents = df[df.isnull().any(1)]\n",
"absents[[\"Classe\", \"Nom\"]+matieres]"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 12,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df = df[~df.isnull().any(1)]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Répartition des notes.\n",
"\n",
"Le DNB blanc était noté sur **325**."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78d789390>"
]
},
"execution_count": 13,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2QAAAEyCAYAAACVoBMLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAEyFJREFUeJzt3X+Ibvl9F/D3p3tTjTtho2wcyk3wFg2B6NJNdoiVSJmJ\nWLfZYhSKJGBsSuUKJiFCBLeCqH+I+08qFWox2pCIbYcQuxiycWuoGUPBpJ0b19790WBIbsle0iyh\neptZS8OuX/+YZ3XcO3Pn3H1+fOY+83rBMPOc+Z5zPuc8H77PvHnOc6bGGAEAAGD1vqe7AAAAgPNK\nIAMAAGgikAEAADQRyAAAAJoIZAAAAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA0OTCMjZ67733jkuX\nLi1j05xzzz//fO6+++7uMlhz+oxl02Msmx5jFfTZrV25cuXbY4zXnTZuKYHs0qVL2d/fX8amOef2\n9vayvb3dXQZrTp+xbHqMZdNjrII+u7Wq+u0p41yyCAAA0EQgAwAAaCKQAQAANBHIAAAAmghkAAAA\nTQQyAACAJgIZAABAE4EMAACgyaRAVlWvrapPVdVvVdUzVfXnll0YAADAurswcdzPJHl8jPFjVfW9\nSf7IEmsCAAA4F04NZFV1T5IfSvK+JBljfDfJd5dbFgAAwPqrMcatB1Tdn+SjSZ5O8gNJriT50Bjj\n+ZeNu5zkcpJsbm4+sLu7u5SCOd8ODg6ysbHRXQZrTp8t19XrN25adt/Fe5a+7lmix1g2PcYq6LNb\n29nZuTLG2Dpt3JRAtpXki0nePsb4UlX9TJLfG2P8g5PW2draGvv7+7dbM5xqb28v29vb3WWw5vTZ\ncl16+LGbll175KGlr3uW6DGWTY+xCvrs1qpqUiCbclOPZ5M8O8b40uzxp5K8dZ7iAAAAmBDIxhi/\nk+QbVfWm2aK/kMPLFwEAAJjD1LssfjDJL8zusPi1JD+xvJIAAADOh0mBbIzxRJJTr38EAABgukn/\nGBoAAIDFE8gAAACaCGQAAABNBDIAAIAmAhkAAEATgQwAAKCJQAYAANBEIAMAAGgikAEAADQRyAAA\nAJoIZAAAAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA0EQgAwAAaCKQAQAANBHIAAAAmghkAAAATQQy\nAACAJgIZAABAE4EMAACgiUAGAADQRCADAABoIpABAAA0EcgAAACaCGQAAABNBDIAAIAmAhkAAEAT\ngQwAAKCJQAYAANBEIAMAAGgikAEAADQRyAAAAJpcmDKoqq4l+U6SF5O8MMbYWmZRAAAA58GkQDaz\nM8b49tIqAQAAOGdcsggAANCkxhinD6r6epL/kWQk+ZdjjI8eM+ZykstJsrm5+cDu7u6CS4Xk4OAg\nGxsb3WWw5pbVZ1ev37hp2X0X71n4fs7Kfk8yTz2rOJZV7MNcxhTz9KIeYxX02a3t7OxcmfJRr6mB\n7OIY43pV/fEkn0vywTHGF04av7W1Nfb392+rYJhib28v29vb3WWw5pbVZ5cefuymZdceeWjh+zkr\n+z3JPPWs4lhWsQ9zGVPM04t6jFXQZ7dWVZMC2aRLFscY12ffn0vyaJK3zVceAAAApwayqrq7ql7z\n0s9JfjjJk8suDAAAYN1NucviZpJHq+ql8b84xnh8qVUBAACcA6cGsjHG15L8wApqAQAAOFfc9h4A\nAKCJQAYAANBEIAMAAGgikAEAADQRyAAAAJoIZAAAAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA0EQg\nAwAAaCKQAQAANBHIAAAAmghkAAAATQQyAACAJgIZAABAE4EMAACgiUAGAADQRCADAABoIpABAAA0\nEcgAAACaCGQAAABNBDIAAIAmAhkAAEATgQwAAKCJQAYAANBEIAMAAGgikAEAADQRyAAAAJoIZAAA\nAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA0GRyIKuqu6rqv1bVZ5ZZEAAAwHlxO++QfSjJM8sqBAAA\n4LyZFMiq6vVJHkryr5dbDgAAwPlRY4zTB1V9Ksk/TfKaJH93jPGjx4y5nORykmxubj6wu7u74FIh\nOTg4yMbGRncZrLll9dnV6zduWnbfxXsWvp+zst+TzFPPKo5lFfu4nR476+dr6n5Xte91Ms/z5/WS\nVdBnt7azs3NljLF12rhTA1lV/WiSd44x/nZVbeeEQHbU1tbW2N/fv516YZK9vb1sb293l8GaW1af\nXXr4sZuWXXvkoYXv56zs9yTz1LOKY1nFPm6nx876+Zq631Xte53M8/x5vWQV9NmtVdWkQDblksW3\nJ/nLVXUtyW6Sd1TVv52zPgAAgHPv1EA2xvipMcbrxxiXkrw7yX8aY/z1pVcGAACw5vwfMgAAgCYX\nbmfwGGMvyd5SKgEAADhnvEMGAADQRCADAABoIpABAAA0EcgAAACaCGQAAABNBDIAAIAmAhkAAEAT\ngQwAAKCJQAYAANBEIAMAAGgikAEAADQRyAAAAJoIZAAAAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA\n0EQgAwAAaCKQAQAANBHIAAAAmghkAAAATQQyAACAJgIZAABAE4EMAACgiUAGAADQRCADAABoIpAB\nAAA0EcgAAACaCGQAAABNBDIAAIAmAhkAAEATgQwAAKCJQAYAANBEIAMAAGhyaiCrqj9cVb9eVf+t\nqp6qqn+8isIAAADW3YUJY/4gyTvGGAdV9aokv1ZV/2GM8cUl1wYAALDWTg1kY4yR5GD28FWzr7HM\nogAAAM6DOsxbpwyquivJlSR/KsnPjjH+3jFjLie5nCSbm5sP7O7uLrhUSA4ODrKxsdFdxtq7ev3G\nTcvuu3jPmV53kds7ODjI12+8eOzv5jmWRW+v67zOa2o9iz6HUy26vuPWP2kuO0t9M9U85+Gk9Tv7\n8yyZ59x4vWQV9Nmt7ezsXBljbJ02blIg+7+Dq16b5NEkHxxjPHnSuK2trbG/vz95uzDV3t5etre3\nu8tYe5cefuymZdceeehMr7vI7e3t7eV9jz9/7O/mOZZFb6/rvM5raj2LPodTLbq+49Y/aS47S30z\n1Tzn4aT1O/vzLJnn3Hi9ZBX02a1V1aRAdlt3WRxj/M8kn0/y4CstDAAAgENT7rL4utk7Y6mqVyf5\ni0l+a9mFAQAArLspd1n8viSfmH2O7HuSfHKM8ZnllgUAALD+ptxl8TeTvGUFtQAAAJwrt/UZMgAA\nABZHIAMAAGgikAEAADQRyAAAAJoIZAAAAE0EMgAAgCYCGQAAQBOBDAAAoIlABgAA0EQgAwAAaCKQ\nAQAANBHIAAAAmghkAAAATQQyAACAJgIZAABAE4EMAACgiUAGAADQRCADAABoIpABAAA0EcgAAACa\nCGQAAABNBDIAAIAmAhkAAEATgQwAAKCJQAYAANBEIAMAAGgikAEAADQRyAAAAJoIZAAAAE0EMgAA\ngCYCGQAAQBOBDAAAoIlABgAA0EQgAwAAaHJqIKuqN1TV56vq6ap6qqo+tIrCAAAA1t2FCWNeSPLh\nMcaXq+o1Sa5U1efGGE8vuTYAAIC1duo7ZGOMb44xvjz7+TtJnklycdmFAQAArLvb+gxZVV1K8pYk\nX1pGMQAAAOdJjTGmDazaSPKfk/yTMcYvH/P7y0kuJ8nm5uYDu7u7i6yTc+7q9RtJks1XJ9/6/cNl\n9128p7GiHi+dh6OWcR6m7ue4cceZWuOij++VHsfRPlu2ec7rPNub5zlZVT3z7nuKVe335fs5ODjI\n12+8uLDtnaTzuT/OWevPKTpfa+Y5vuPmsfP4uslyHRwcZGNjo7uMM2tnZ+fKGGPrtHGTAllVvSrJ\nZ5L8yhjjp08bv7W1Nfb39ycVClNcevixJMmH73shH7l6+NHHa4881FlSi5fOw1HLOA9T93PcuONM\nrXHRx/dKj+Nony3bPOd1nu3N85ysqp559z3Fqvb78v3s7e3lfY8/v7DtnaTzuT/OWevPKTpfa+Y5\nvuPmsfP4usly7e3tZXt
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa78d846ef0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[\"total\"].hist(bins=150, figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Quelques statistiques!\n",
"\n",
"Pour les non anglophones *mean* signifie *moyenne*, *std* (standart deviation) signifie *écart type*\n",
"\n",
"Barèmes:\n",
"Français 100 HG 50 Math 100 SVT 25 Physique Chimie 25 Techno 25"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Français</th>\n",
" <th>HG</th>\n",
" <th>Maths</th>\n",
" <th>SVT</th>\n",
" <th>Physique</th>\n",
" <th>Techno</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>count</th>\n",
" <td>178.00</td>\n",
" <td>178.00</td>\n",
" <td>178.00</td>\n",
" <td>178.00</td>\n",
" <td>178.00</td>\n",
" <td>178.00</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>mean</th>\n",
" <td>45.53</td>\n",
" <td>22.56</td>\n",
" <td>34.69</td>\n",
" <td>12.77</td>\n",
" <td>10.56</td>\n",
" <td>12.69</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>std</th>\n",
" <td>15.83</td>\n",
" <td>9.13</td>\n",
" <td>17.26</td>\n",
" <td>5.07</td>\n",
" <td>4.91</td>\n",
" <td>5.02</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>min</th>\n",
" <td>2.00</td>\n",
" <td>0.00</td>\n",
" <td>1.00</td>\n",
" <td>2.00</td>\n",
" <td>2.00</td>\n",
" <td>2.50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td>37.50</td>\n",
" <td>15.25</td>\n",
" <td>23.00</td>\n",
" <td>9.12</td>\n",
" <td>6.00</td>\n",
" <td>8.50</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>50%</th>\n",
" <td>47.00</td>\n",
" <td>23.00</td>\n",
" <td>30.00</td>\n",
" <td>12.00</td>\n",
" <td>10.00</td>\n",
" <td>12.50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>55.38</td>\n",
" <td>28.75</td>\n",
" <td>42.75</td>\n",
" <td>16.00</td>\n",
" <td>14.00</td>\n",
" <td>16.50</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td>88.00</td>\n",
" <td>43.00</td>\n",
" <td>90.00</td>\n",
" <td>25.00</td>\n",
" <td>24.00</td>\n",
" <td>23.50</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
2018-04-12 18:06:58 +00:00
" Français HG Maths SVT Physique Techno\n",
"count 178.00 178.00 178.00 178.00 178.00 178.00\n",
"mean 45.53 22.56 34.69 12.77 10.56 12.69\n",
"std 15.83 9.13 17.26 5.07 4.91 5.02\n",
"min 2.00 0.00 1.00 2.00 2.00 2.50\n",
"25% 37.50 15.25 23.00 9.12 6.00 8.50\n",
"50% 47.00 23.00 30.00 12.00 10.00 12.50\n",
"75% 55.38 28.75 42.75 16.00 14.00 16.50\n",
"max 88.00 43.00 90.00 25.00 24.00 23.50"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 14,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
2018-04-12 18:06:58 +00:00
"round(df[matieres].describe(), 2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Répartition des notes par matières\n",
"\n",
"Vous allez enfin retrouver les boites à moustaches!\n",
"\n",
"*Les notes ont été normalisées pour pouvoir comparer les épreuves*"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 15,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
2018-04-12 18:06:58 +00:00
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78d76bf98>"
]
},
"execution_count": 15,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA20AAAEzCAYAAACi6etkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+c5XddH/rXm13IpjFErrHbSkKWW1I7m0UQ90aL28uM\nUW8iFugDEYZqxcc8iOkt01uX3sduGS+/ZCRbra1GNCbdKFdliEpLUzYEapiprqglEIGQKd6U8COh\nLQISWEyW7Pq5f5yzy+xmf5zJnNnznZnn8/GYx+Oc7/me73nPmc+c8319P5/v51uttQAAANBNTxh1\nAQAAAJye0AYAANBhQhsAAECHCW0AAAAdJrQBAAB0mNAGAADQYUIbAABAhwltAAAAHSa0AQAAdNjm\nUb3wxRdf3LZt2zaql++sr371q7ngggtGXQZrgLbCcmgvDEpbYTm0FwalrZzaBz/4wc+31r75bOuN\nLLRt27Ytd91116hevrMWFhYyPj4+6jJYA7QVlkN7YVDaCsuhvTAobeXUqupTg6xneCQAAECHCW0A\nAAAdJrQBAAB0mNAGAADQYUIbAABAhwltAAAAHSa0AQAAdNhZQ1tV3VJVn6uqe07zeFXVL1bVfVX1\nkap6zvDLBAAA2JgG6Wn79SRXn+Hxa5Jc3v+5NsmvrLwsAAAAkgFCW2vt95N88QyrvDDJ/9t6/jjJ\nN1bV3xxWgQAAABvZ5iFs46lJPrPk/gP9Zf/95BWr6tr0euOydevWLCwsDOHl15dDhw55XxiItsJy\naC8bw8TExKhLOMH8/PyoS2CV+WxhUNrKygwjtA2stXZTkpuSZOfOnW18fPxcvvyasLCwEO8Lg9BW\nWA7tZWNora14G9v2Hsgnr3/+EKphI/DZwqC0lZUZxuyRDya5dMn9S/rLAAAAWKFhhLbbkvyj/iyS\n35XkodbaY4ZGAgAAsHxnHR5ZVXNJxpNcXFUPJHldkicmSWvtxiS3J/mBJPcl+cskP75axQIAAGw0\nZw1trbXJszzekvyToVUEAADAccMYHgkAAMAqEdoAAAA6TGgDAADoMKENAACgw87pxbUBABi9qhp1\nCScYxoXhYT3T0wYAsMG01obyc9medw1lO8CZCW0AAAAdJrQBAAB0mNAGAADQYSYiAQAATsvENaOn\npw0AADitLk1asxEDWyK0AQAAdJrQBgAA0GFCGwAAQIcJbQAAAB0mtAEAAHSY0Aawjk1PT2fLli2Z\nmJjIli1bMj09PeqSAIBlcp02gHVqeno6N954Y/bt25ft27fn3nvvzZ49e5IkN9xww4irAwAGpacN\nYJ26+eabs2/fvuzevTtbtmzJ7t27s2/fvtx8882jLg0AWAahDWCdOnz4cJ7ylKdkx44dueqqq7Jj\nx4485SlPyeHDh0ddGgCwDIZHAqxTmzdvzqtf/eq84x3vyNGjR7Np06a8+MUvzubNPvoBYC3R09YR\nc3NzJxwNn5ubG3VJwBr35Cc/OV/+8pdz991358iRI7n77rvz5S9/OU9+8pNHXRoAsAwOt3bA3Nxc\nZmZmsn///uNHw6emppIkk5OTI64OWKu+9KUv5Sd+4ifymte8JocPH855552Xa6+9Nr/6q7866tIA\ngGXQ09YBs7Oz2b9/fyYmJrJ58+ZMTExk//79mZ2dHXVpwBo2NjaWl7zkJXnkkUcyPz+fRx55JC95\nyUsyNjY26tIAgGUQ2jpgcXExu3btOmHZrl27sri4OKKKgPVgZmYmU1NTmZ+fz5EjRzI/P5+pqanM\nzMyMujQAYBkMj+yAsbGxHDx4MBMTE8eXHTx40NFwYEWODa+enp7O4uJixsbGMjs7a9g1AKwxeto6\nwNFwYLVMTk7mnnvuyZ133pl77rlHYAOANUhPWwdMTk7m/e9/f6655prjkwW88pWvtHMFAAAIbV0w\nNzeXAwcO5N3vfvcJs0c+97nPFdwAAGCDMzyyA8weufFU1Yp/JiYmhrKdqhr12wEAwBkIbR1g9siN\np7W24p/L9rxrKNtprY367QAA4AyEtg44NnvkUmaPBAAAEqGtE8weCQAAnI6JSDrAtZQAAIDTEdo6\nYnJyMpOTk1lYWMj4+PioywEAADrC8EgAAIAOE9oAAAA6TGgDAADoMKENAACgw4Q2AACADhsotFXV\n1VX18aq6r6r2nuLxp1XVfFXdXVUfqaofGH6pAAAAG89ZQ1tVbUryliTXJNmeZLKqtp+02k8l+e3W\n2rcneVmSXx52oQAs39zcXHbs2JGrrroqO3bsyNzc3KhLAgCWaZDrtF2Z5L7W2ieSpKrenuSFSe5d\nsk5L8uT+7YuSfHaYRQKwfHNzc5mZmcn+/ftz9OjRbNq0KVNTU0l614YEANaGQYZHPjXJZ5bcf6C/\nbKnXJ/mRqnogye1JpodSHQCP2+zsbPbv35+JiYls3rw5ExMT2b9/f2ZnZ0ddGgCwDIP0tA1iMsmv\nt9b+VVX93SS/UVU7Wmt/tXSlqro2ybVJsnXr1iwsLAzp5dePQ4cOeV8YmLbCmSwuLubo0aNZWFg4\n/tly9OjRLC4uajuckfbBcmgvDEpbefwGCW0PJrl0yf1L+suWmkpydZK01v6oqrYkuTjJ55au1Fq7\nKclNSbJz5842Pj7++KpexxYWFuJ9YSB3HNBWOKOxsbFs2rQp4+Pjxz9b5ufnMzY2pu1wej5bWA7t\nhUFpKysyyPDIDyS5vKqeXlVPSm+ikdtOWufTSa5KkqoaS7IlyZ8Ps1AAlmdmZiZTU1OZn5/PkSNH\nMj8/n6mpqczMzIy6NABgGc7a09ZaO1JVr0ryniSbktzSWvtYVb0xyV2ttduSvDrJzVX1k+lNSvKK\n1lpbzcIBOLNjk41MT09ncXExY2NjmZ2dNQkJAKwxA53T1lq7Pb0JRpYue+2S2/cm+e7hlgYAAMCw\nJiIBoGNM+Q8A68Mg57QBsAaZ8h8A1gehDWCdWlxczK5du05YtmvXriwuLo6oIgDg8RDaANapsbGx\nHDx48IRlBw8ezNjY2IgqAgAeD+e0AaxTMzMzeelLX5oLLrggn/rUp3LZZZflq1/9an7hF35h1KUB\nAMugpw1gA6iqUZcAADxOQtuQVNVQfiYmJoayHYDZ2dnceuutuf/++3PnnXfm/vvvz6233moiEgBY\nY4S2IWmtDeXnsj3vGsp2AExEAgDrg9AGsE6ZiAQA1gcTkQCsU0snIvn0pz+dpz3taSYiAYA1SE8b\nwAZg2DQArF1CG8A6tXQikve9730mIgGANUpoA1inTEQCAOuD0AawTpmIBADWB6ENYJ2amZnJ1NRU\n5ufnc+TIkczPz2dqaiozMzOjLg0AWAazRwJ0WFWteBvf8z3fc8L9l7/85Xn5y1/+uLZlQhMAOPf0\ntAF0WGttKD+X7XnXULYDAJx7QhsAAECHCW0AAAAdJrQBAAB0mNAGAADQYUIbAABAhwltAAAAHSa0\nAQAAdJjQBgAA0GFCGwAAQIcJbQAAAB0mtAEAAHSY0AYAANBhm0ddAAAAMHzPesN789DDj466jOO2\n7T0w6hKSJBed/8R8+HXfP+oylkVoAwCAdeihhx/NJ69//qjLSJIsLCxkfHx81GUk6U54XA7DIwEA\nADpMaAMAAOgwoQ0AAKDDnNMGACNmsoBTW4uTBQCsBqENAEbMZAGn1pXwCDBqhkcCAAB0mNAGAADQ\nYUIbAABAhwltAAAAHSa0AQAAdNhAoa2qrq6qj1fVfVW19zTr/HBV3VtVH6uqtw23TAAAgI3prFP+\nV9WmJG9J8n1JHkjygaq6rbV275J1Lk/yL5J8d2vtL6rqr69WwQAAABvJID1tVya5r7X2idba15K8\nPckLT1rnlUne0lr7iyRprX1uuGUCAABsTINcXPupST6z5P4DSb7zpHX+dpJU1R8m2ZTk9a21O07e\nUFVdm+TaJNm6dWsWFhYeR8nrn/eFQWkrLIf20m1d+fscOnSoM7Uk3XlfOD1/o27ryt/HZ8vKDBLa\nBt3O5UnGk1yS5Per6pm
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa78b64f4e0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[norm_matieres].boxplot(figsize=(15,5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"source": [
"Les plus motivés pourront faire *flèche du bas* pour voir pleins de beaux graphiques qui ne disent pas grand chose (mais j'aime qu'on me fasse mentir)."
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
"### Y a-t-il un lien entre la réussite dans une matière et dans une autre?\n",
"\n",
"Dans les nuages de points, chaque point correspond à une élèves.\n",
"\n",
"On compage ses notes dans deux matières à chaque fois. L'idée est de voir si la réussite dans une matière est liée à la réussite dans une autre (elles sont **corrélées**) ou si au contraire, il n'y a pas de lien. Elles sont fortement corrélées quand les points sont regroupés. Si les points sont éclatés, la réussite dans une matière ne semble pas de rapport avec la réussite dans une autre.\n",
"\n",
"Les graphiques du milieu montre la répartition de toutes les notes dans chaque matière."
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"from pandas.plotting import scatter_matrix"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"scrolled": false,
"slideshow": {
"slide_type": "subslide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3YAAANgCAYAAABgIvoLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXlwJNd95/nJrPsuAIUbDaDR6Ps+eTSbh0ha1EGJoizJ\nkiXZGlsOH7M769iZXU/E/Lm74YmNjY1Zb+xueDcsz8ojr2XLOilSFiWS4k323ehu9IFuNK4qVBXq\nvrMyc/+oQjXQKABVAKoBdL/PHyRQXVn5UPny5fu99/19f5Ku6wgEAoFAIBAIBAKBYPMir3cDBAKB\nQCAQCAQCgUCwOkRgJxAIBAKBQCAQCASbHBHYCQQCgUAgEAgEAsEmRwR2AoFAIBAIBAKBQLDJEYGd\nQCAQCAQCgUAgEGxyRGAnEAgEAoFAIBAIBJscEdgJBAKBQCAQCAQCwSZHBHYCgUAgEAgEAoFAsMkR\ngZ1AIBAIBAKBQCAQbHKM692AxfD5fHp/f/96N0OwSRgdHUX0F0EtiL4iqAfRXwS1IvqKoB5EfxHU\nypkzZ8K6rrfW8t4NG9j19/dz+vTp9W6GYJNw7Ngx0V8aTE5RMRlkDLK03k1ZFaKvPPjkFBWzQUZe\ng74q+svDRbagYjXJSFL9fUf0lcahaToFVcNqMqx3U9YM0V/uHzlFxShLGA2bU6goSdKdWt+7YQM7\ngUCwcbg8FeeXV6ZxW0187ZHeB+rhKniwOHMnwm+uh2l1WfjK8S2YNumDXHD/eWM4yPnxGH0tdl4+\n0rPezRGUKaoa/3B6nGAizxPbfRzvb17vJgk2ETemk/z8UgCHxcDvnOjFaXmwQx/xxBMIBMtyK5RG\n1yGeVQin8uvdHIFgUUaCaQBCyTyJrLLOrRFsJkZCKQDuzGRQVG2dWyOYJZkrEkyUnjsjwdQ6t0aw\n2bgVTqPpOslckelEbr2b03BEYCcQCJblaF8TPqeZnR0uOj229W6OQLAoJ7Y20+wws7/bQ7PDvN7N\nEWwiHh1ooclu4pGBZrHTu4Hw2k0c6Cndzye2it06QX0c3uLF57Iw0Oqgt9m+3s1pOA/2fqRAIFgT\nurw2vvFYf+X3OzNpbGYDbS7r+jVKIKhCv89Bv8+xomMVVePOTIZ2twWX1bTGLRNsdPZ1e9jX7an5\n/cFkjmxBpa9lZf1NUBuSJHGsr5m+lrz4rgWLklNUJqIZur12bOa76SJtbivfeLRvHVt2fxGBnUAg\nqIuzY1HeuhZCliS+emILbW4R3AkeDF4dCjASTOGwGPjWya1i10awKMFEjr//aBxN13lqZytHepvW\nu0kPLDlF5XsfjZFTVHZ3unlhX8d6N0mwAfnns5NMJ3L4nOZ5C9EPGyKw22T0/8UrdR8z+pefaUBL\nBA8ryVwRAE3XSeWLtK1zewSCtSJV7tvZgoaq6QiPIMFipPJFNF0H7o6JgsZQUDXyRRUofe8CQTWS\nuVJOdeIhvx9FYCcQCOrika3NaLqO02Jk6wolbwLBRuT5Pe2cH4/R32IXzq+CJdnqc/DEdh+pfJFH\nRN5XQ3FbTXxybwcT0SzH+sTOqKA6nznQyZWpBLs73evdlHVFBHYCgaAurCYDz+wU+3SCB49Wl4Xn\n97SvdzMEmwBJkoTt/n1kd6f7oZ+wC5amp8lOT9ODb46yHCKBQCAQCAQCgUAgEAg2OSKwEwgEAoFA\nIBAIBIJNTsMCO0mS7JIkvSJJ0puSJP1YkiSLJEn/qyRJb0uS9J8adV6BQCAQCAQCgUAgeNho5I7d\nC8CHuq4/DXwE/AXg1HX9FGCWJOl4A88tEAgEAoFAIBAIBA8NjQzsRoBZyzwvoAO/LP/+OvBYA88t\nEAgEAoFAIBAIBA8NjQzsbgCPSZJ0GTgGFIFE+d/ilIK9eUiS9EeSJJ2WJOl0KBRqYNMEAoFAIBAI\nBAKB4MGhkYHd7wE/1XV9L/AKYAJmvWrdQOzeA3Rd/2td14/pun6stbW1gU0TCAQCgUAgEAgEggeH\nRgZ2EhAp/xwu///Z8v+fAz5o4LkFAoFAIBAIBAKB4KGhkYHd94AvS5L0JvC7wF8BOUmS3gZUXdc/\nauC5BQKBQCAQCAQCgeChwdioD9Z1PQZ88p6X/02jzicQCAQCgUAgEAgEDyuiQLlAINg06LrOeCRD\nPKusd1M2HfmiythMhkJRW++mCATzCMRzzKTy690MQQOIZxQmopn1bobgAUL0qaVp2I6dQCBYH676\nEyRzRQ5t8WI2PlhrN++PzPDh7Qhmo8w3H+vDZTWtd5M2Df90ZoJgIk+318aXj29Z9v3+eJbboTS7\nO900Ocz3oYWC1ZDOF7kwEaPLY6Pf51j+gA3ClakEv7gcQJYkvny8h06Pbb2bJACGJuPkFJVDW7wY\nDSt7jsQzCn/34R0KRY3Ht7XwyEDLGrdS8LARzyh894NRFFXn5KCPE1ub160tmqZzfiKGLEkc7PEg\nSdK6tWUuIrATCB4gJqIZXhsKAJBVVJ7asTndZUdCKc6MRhlsd3Kkt6nyeiRTAKBQ1EjnVRHY1UEs\no6CoGu/cDGO3GHhudztWk6Hqe1VN55/PTlIoaoyE03zj0b773FpBvbx+dZpboTSyJPGtJ/pxr/Le\nSOYUfj0cxGyQeXZ3e8MWiaLle1rTdWIZRQR2G4CbwRS/vDINgKaz4slzMq9UFAKz1/l+ceZOlJFg\niuNbm9m6iRY6HkR0XefNayFm0gWe3tmKz2lZ8WclcgqKqgMQSd/fPnUvlybjvHWtVJrNKEvs6/as\na3tmEYGdQPAAYZRlJAl0HUzyxlg9WglvXQsRzypMxrLs6/JUJpWnBlsxyhI+p4UOj3WdW7m5+NS+\nDn5yYYomu4kb0ym6vTYOzwma5yIBhnL/2cz96GHCVN5VkSWQ12Dl+MJ4nFuhNAC9LXb2djVm0nK0\nr4lMQcVqktnZ7mrIOQT1YTLc7T+GVdz/PU12Tg76iKTzPD7oW4um1UROUfnN9dKEO3MtyFbf1vt2\nbsFCJqJZzo+XKpx9eCvCZw50rviztjTbeXxbC9GMwsnB9d0BNs65T0wr3NVuBCKwEwgeIDo8Vl4+\n3EMyr7Crw738ARuULq+NeFah3W2dN8nw2E28sG/lD4WHmYFWJy8f7uFH5yeRYMnAWJYlvnxsC+OR\nDINtzvvXSMGKeXZ3Gz1NNtrdVpyW1T/aO71WJKm0Et3matwiitVk4Pk97Q37fEH99LU4+PyhLvJF\njV0dqwu210MqZzbItLoshJJ5urxiB3i9aXaYsZsNZAoqXd7VjyUbRdK7t8uDySAjSzDYtnEWpURg\nJxA8YPS22Nfkc6ZiWd4bmaHba+Oxbfd3IP3k3naO9TfhtZk2jG79QaC3xc63TvYjSdKyk/9mh5nm\nZXLrztyJciuU4sTWZvpahNxpPbEYDRzo8a7Z521rdfKtk1sxyhKONQgU14OcovLr4SCarvPsrnZs\n5urSY8FCBlo374KOLEt85fgWElll2TFslqHJOFf9CQ5u8bJD7ByvKQ6Lkd97vJ9sQW1ovva1QJKL\nEzH2dnnY03V/FrY3Yl/ZnKO1QCBoOO/cCDMZyzIeybCrw3VfDTQkSVqVDl+wOGuVl5gt3JU7ZZUQ\n33xMBHYPGh7b5s5hvepPcC2QBKDNZV1XowXB/cVkkGmp8Rmi6zq/Hg6iajrhVGFDTtY3O1aTYdGc\n7rXiV8PT5BWNQDx33wK7jcjGEYUKBIINxayExWMzbdoVe0HjsBhlfM5SsC8MLwQbkXa3FYMsIUsS\nHW6RkyuojiRJFWn6WkgFBetDV/k51PmQy2/FbE0gEMxD0zRkWeaJ7T52dbpwWY0PXNkEQW3our6o\nFFaWJX7nRC+xjFIJ8JY7phHtEGwcGnmdVvLZXV4b3zrZjw41u4SKvrZxWeza1HvNqr3/5cPdRDO1\nSzcFG48XD3YRSRcafg1XO0Y0eowRgZ1AIKjwn98b5bWhALs7XfyHz+yuSw4Zzyj845lxiprOy4e7\naRMr5JuaVy/5uT5dyp9
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa78b35ac50>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ax = scatter_matrix(df[matieres],\n",
" alpha=0.5,\n",
" figsize=(15, 15),\n",
" #diagonal='kde',\n",
" )"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
" Une autre version mais chaque couleur correspond à une classe.\n"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {
"scrolled": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABGsAAAQwCAYAAABSYNOpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XeQJFl+2PfvS1OV5U17M97P7s6amfUA9wzM4bA4CCQh\nAZShEAIBSUEpKCkkQUEFg0IEJEoRAkUhACkQCgkSSRwFhkjccQHcETgcFrfmdmdm7Zgd22PaTJvy\nLisrK5/+qPZmpsf0TJvfJ6Jjp3Oqq1/N/vLly1++93tKa40QQgghhBBCCCGE2ByMJ90AIYQQQggh\nhBBCCLFAkjVCCCGEEEIIIYQQm4gka4QQQgghhBBCCCE2EUnWCCGEEEIIIYQQQmwikqwRQgghhBBC\nCCGE2EQkWSOEEEIIIYQQQgixiUiyRgghhBBCCCGEEGITkWSNEEIIIYQQQgghxCYiyRohhBBCCCGE\nEEKITWRLJmu+9rWvaUC+5OtRfD02Erfy9Qi/HhuJW/l6hF+PjcStfD3Cr8dG4la+HvHXYyFxK1+P\n+EsssiWTNTMzM0+6CULcN4lbsRVJ3IqtSOJWbEUSt2IrkrgVYuNsyWSNEEIIIYQQQgghxHYlyRoh\nhBBCCCGEEEKITUSSNUIIIYQQQgghhBCbiCRrhBBCCCGEEEIIITYRSdbsJG3/SbdACCGEEEIIIYQQ\n9yDJmp1Aa/jnvwS/0QeX//WTbo0Qj4zWmnbVw8+7tKseWsuOf2J7k5gXW5XErnjcJObEViWxK+ZY\nT7oB4jG49Mdw/l90/vwn/xUc+nFQ6sm2SYiHpLWmNVbFHSmjXR/lWDj7kthDcZTEt9iGJObFViWx\nKx43iTmxVUnsisVkZs1O8PE/hcQA/PRvQmEEJs896RYJ8dCCWmv+QgagXR93pExQaz3hlgmxMSTm\nxVYlsSseN4k5sVVJ7IrFJFmz3Xk1uPqn8NRfhaNvdo5d+/6TbZMQj4D2gvkL2fwx10d7wRNqkRAb\nS2JebFUSu+Jxk5gTW5XErlhMkjXb3c33oO3BoR+DRB8kh2HikyfdKiEemgoZKGduJadGe21QoNGy\ntldsS0tjfvaYY6FCC5dyWecuNqN7xa7ErXjUOjFnor02QcNHe22UYy7pL4XYTOb6Qe0HKFMBC/3g\n8mu92DmkZs12N/I2mCHY9Urn+8HnYFySNWLrM2I2zr4k7kgJf6pO4Ac4vWnc6yXC/b6s7RXbzkLM\nL13HbsRsQNa5i83rbrErcSs2gopahPpiVMerBKUmRipM/FAGFZVbH7H5LO4HMcFMh2lN1lCWgXLs\nJdd6sbNIj7Xd3f4QBp+HULTzff8z8MUfQcsF23mybRPiISilOoP5qEWrOwJeG7/WQtd83EYbMx3G\njIeedDOFeGTmYt5Mh9FegAoZGDF7/oZ2rXXuci6IJ+1usduuehK34pHTdZ9WuUn0aBZMA9oBrXIT\nu+6DxJXYZJZfv9tAaHcKq8fBjNpLrvViZ5FkzXbmN2H8Y3j5VxeOdR0EdKfQcO+xJ9Y0IR4FpRQK\nRWu0uuS4rO0V25VSas0bWFnnLjaztWJX4lZsBO0FBIUmy6NI4kpsRsv7QV3zadWqhAZikrTe4WTx\n23Z251ynXs3QqYVjXQc6/81dfTJtEuIRW08dDyF2AjkXxFYkcSs2gsSV2EokXsVaJAK2s4mPO/9J\nHeR2+XbnWFaSNWJ7mauFMHeRW17HQ4idQs4FsRVJ3IqNIHElthKJV7EWWQa1nY1/wrSV4sf+5D/G\nClX5g5/5JkeyRyDaBcVbT7p1QjwS96rjIcROIeeC2IokbsVGkLgSW4nEq1iLzKzZxqo3P+af2P0Y\noQIBLX7zg/+j8xepYSiNPtnGCfEIzdVCsLIOZjwkFzexY8m5ILYiiVuxESSuxFYi8SpWs+HJGqXU\n15RSl5RSV5VSv7bK3+9WSn1fKfWxUuozpdTXN7pNO0LbJ1y4xPvxMOlwBlV7ng+nfkA7aENqFxRv\nP+kWCiGEEEIIIYQQYhUbmqxRSpnAbwM/BRwHflEpdXzZy/5b4A+01s8DvwD8zka2aadoTV/G1i0m\nYwEv9D7PqZ7X8KlxYeby7Mya26D1k26mEEIIIYQQQgghltnomTUvAVe11te11h7wz4CfXfYaDSRn\n/5wCxje4TTvCzQtnaChFQVU4kj3C1w6/DMBbl37YSdZ4VXCLT7iVQgghhBBCCCGEWG6jkzVDwOL1\nNqOzxxb7+8C/o5QaBf4Y+E82uE07Qunmp1y2Q2g0hzOHefPoM+h2lB+OfQLJwc6LKneebCOFEEII\nIYQQQgixwmYoMPyLwO9prYeBrwP/WCm1ol1KqV9RSp1RSp2Znp5+7I3casyZi3wa6gFgT3IP0bBF\njF2M169DvL/zosrEE2zhziBxK7YiiVuxFUnciq1I4lZsRRK3QjweG52sGQN2Lfp+ePbYYv8B8AcA\nWuv3AQfoXv5GWuvf1Vqf0lqf6unp2aDmbh/Z+nVuRLMADMU7k5mGYvtpqDHcyOy/n8ys2XASt2Ir\nkrgVW5HErdiKJG7FViRxK8TjsdHJmtPAIaXUPqVUiE4B4W8ve80t4KsASqljdJI1kqJ9CKVKlcFg\nkslojKyTJWpHAXim5wjKaPGDXKnzQplZI4QQQgghhBBCbDobmqzRWvvA3wa+C1yks+vTeaXUryul\nvjH7sv8C+FtKqU+BbwL/vtayTdHDuH3tPJYKyIUVw/Hh+eOv734agPfGb0A4JTNrhBBCCCGEEEKI\nTcja6F+gtf5jOoWDFx/7e4v+fAF4faPbsZPkb34OQNHweCrWP3/85V1HAbiYuwKJPplZIzYNrTV5\nN4/ruziWQ9bJopR6ou1p5/MErovhOJjZJ9sesXncLTY2WxyL7etxxZr0heJxWW9MS0yK7eJRxrKM\nP7avDU/WiMfPm7yCBvJ+hd5o7/zxVDiFpVPcrt6AeB9UZbWZePK01lzMXeTs1FmqXpV4KM7J3pMc\n6zr22C40WmtyNQ/XaxMNm0RuXKV+5gxBpYqRiBM9dQrn+HG58O1wWmvcCxeonTlDLVeEWJzUyy+S\nPPE0SqknHsdiZ7jfPnNx/+aETLpioXXF5Fy8S18oNtp6Y/pRxuSDnhdC3Mt6YutRx7KMP7YvSdZs\nQ6HSCKNGhobfoC/at+TvMvYwU81RdLIPNfHJE2qhEAvybp6zU2epeBUAKl6Fs1Nn6Yv10RXp2vDf\nr7Xm3FiJD0fyVFyf17oM0u+9R1q7KBRBuUL9zBns/n6sro1vj9i82vk8tTNnmBydZqzYoOkXSefq\n7E914fQ7TzSOxc5xP33m8v4t4Vi8tC/L00Opew7i2/l850ai3Pk90heKjbLemH5UMfkw54UQd7Pe\n2HqU/euTHkeLjbUZtu4Wj1i6cYur0UEAeqJLK7Tviu8Fe4qqlZGZNWJTcH2XqlddcqzqVXF997H8\n/lzN48ORPGXXRwN2u8WNW5M0vPb8a4JKlcB9PO0Rm1fgutRyxdlETQBAcaZAsVCh5NafaByLneN+\n+szl/VvZ9flwJE+u5t3z9wSuS1BZ+nukLxQbYb0x/ahi8mHOCyHuZr2x9Sj71yc9jhYbS5I120yr\nHTDQHudOvJOkWbwMCuBY9yGU2eSLdgi8CrQaT6KZQsxzLId4KL7kWDwUx7GcNX9Ga0276uHnXdpV\nj4epSe56bSquP/99VZsYiQR+e+E9jUQcw1m7PWJnMBwHYvH5RA1AJJOi4Bsoba+I4+H4MEk/9kji\nVIg599NnLu/fACquj7soGb0Ww3EwEkt/z3r6wkfZP4udYb0x/aAxudy9zguJYfGg1tvnrhbL1vAw\nyr7/McODjKPF1iHJmm1mfHKGHlWikMgC0BNZOrPmxcFOkeGPvFbnQHXqsbZPiOWyTpaTvSdJhBIo\nFIlQgpO9J8k62VVfr7WmNVal9vE0tbOT1D6epjVWfeDBlBMySTgLK0JHfJu+11/GyaRAKYxkguip\nU5jZ1dsjdg4zmyX18ou
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa789ad2208>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig = sns.pairplot(df,\n",
" vars=norm_matieres,\n",
" hue=\"Classe\",\n",
" diag_kind=\"kde\",\n",
" plot_kws={'alpha':0.5,},\n",
" )\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# Comparaison des classes entre elles\n",
"\n",
"Parce que chaque prof principale aime que sa classe soit la meilleure!\n",
"\n",
"Mais rappelez vous, la comparaison des classes entre elle n'a pas beaucoup d'interet pour juger les élèves. Chaque classe n'a pas été corrigée par le même correcteur et on sait tous à quel point les autres profs sont pas sympas avec nos classes!"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "subslide"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Score total"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"bp_data = df[[\"total\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1)\n",
"bp_data.columns = bp_data.columns.droplevel()"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa782edc9e8>"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3AAAAE/CAYAAAAHeyFHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHulJREFUeJzt3X2QZWddJ/DvbzMJpkjkLTqEJGZEo3YYhOgsxRaj9jiI\nCLsE1KVoUKI2xq1KAq66ZLDVGN0ug6KsokUZbcuwakdcEVIEs7zYXdRQAgKSAGlZgiaSkBdBCBkS\nQzI8+0ffkc4w6em3uWfOvZ9P1a25fe459/md/k3PzHfOc55brbUAAABw/PsPXRcAAADA2ghwAAAA\nPSHAAQAA9IQABwAA0BMCHAAAQE8IcAAAAD0hwAHQa1X1NVXVqurMNe5/RVX94bGu67AxH1FVB6rq\nCcMcF4DRI8ABsOUGYeXQ48tVdd+Kr19ylGOfXVU3DavWYWit3d9aO6W19umj7bveQArAeNnWdQEA\njJ7W2imHnlfVzUle1lp7Z3cVAcBocAUOgKGrqpOr6veq6vaqurWqfqOqTqyqxyX5qyRPXHHF7nFV\n9Yyqel9Vfb6qPl1Vr62qNf0nZFV9c1W9p6ruqaq/TvKYw17/rhXv/aGqesYq73VHVb2yqv6hqv61\nqq6sqkeseP2iqvpkVX22qt5UVdsH2x9yVa2qrq6q/1VV/3dQ13uq6uzB27x78OvHB+f//Kp6fFVd\nN6jxs1X1N2v+ZgMwUgQ4ALpweZJvT/LkJN+ZZDLJK1trn03ygiT/OJhyeMpg2wNJLk7yuCTfleS/\nJHnZ0QapqkryF1kORY9L8pokP7ri9R1J3pxkJsljk/xCkjdX1WMOf68VppJ8b5JvTXJekv8xeK/n\nJPnFQf1nJPlMkv+9yvu8OMmrBuPePvieJMl3D3791sH5vznJpUk+nuS0JKcn+eWjnDoAI0qAA6AL\nL0lyWWvtM621O5P8z6wIVodrrb2/tfZ3rbWDrbVPJvnDJN+zhnHOSTKR5PLW2pdaa+9Kct2K1y9I\n8qbW2jtba19urb0tyY1JnrXKe/52a+3TrbV/SfJrWQ50h87pytbaDa21f0vyyiTPrKrHP8z7vLG1\n9qHW2gNJ/izJU1cZ84EkT0jyDYPzePcq+wIwwgQ4AIZqcFXs8UluWbH5lixftXq4Y86tqr+uqjur\n6gtJfinLV6OO5glJ/mUQqFaOdcjZSX5kMDXx81X1+SS7Bsc9nE8d9l6H9n3CyvdurX0+yRdWOa87\nVjy/N8kpD7Nfkswm+XSShaq6qap+ZpV9ARhhAhwAQ9Vaa1kOL2ev2PwNSW47tMsRDvuDJB9K8k2t\nta9N8itJag3D3Z7ktKr6msPGOuRTSf6wtfboFY9HttZeu8p7nnXYex1aWfLTWXFOVfXoJF+74rzW\n6qvOv7V2d2vtFa21s5P8UJJfWO1ePQBGlwAHQBfmk1w2WKDk67N8D9qfDF67M8nXV9XKK1KnJrm7\ntXagqp6U5CfXOM7/y/K9Y79YVSdV1Z4kz17x+lVJ/mtV7a2qEwaLq+xdZdpjkry8qk6vqtOS7Evy\n5yvO6SeraucgMF6R5G9aa3c83BsdSWvt/iR3J3nioW1V9byqeuLg6uXdSQ4m+fJ63heA0SDAAdCF\nX8ryvWYfS/LhJO9J8uuD165Pck2SWwbTGh+b5L8neVlVHUjye/lKaFrV4GrfC5PsSfKvWb4v7U9W\nvP6PWb6idXmWFx25Jckrsvrfj1cnWUjyiSQfOVR3a+2tWb4n7posX417fFa5r+8ofinJXwzO/3lZ\nvo9vIck9WV6Q5TWttb/d4HsD0GO1/HcbAHA0VXVHkh9ure3vuhYAxpMrcAAAAD0hwAEAAPSEKZQA\nAAA94QocAABATwhwAAAAPbGt6wKS5LTTTms7duzouoyh+eIXv5hHPvKRXZfBMaK/o0tvR5v+ji69\nHW36O7rGrbcf/OAHP9Na+7qj7XdcBLgdO3bkAx/4QNdlDM3i4mImJye7LoNjRH9Hl96ONv0dXXo7\n2vR3dI1bb6vqlrXsZwolAABATwhwAAAAPSHAAQAA9IQABwAA0BMCHAAAQE8IcAAAAD0hwAEAAPSE\nAAcAANATAhwAAEBPCHAAAAA9sa3rAgAAgNFUVZ2N3VrrbOxjyRU4AADgmGitbfhx9qVv3dTxo0qA\nAwAA6AkBDgAAoCcEOAAAgJ6wiMkGuSETAAAYNlfgNsgNmQAAwLAJcAAAAD1x1ABXVWdV1UJV3VhV\nH6uqVwy2/3JV3VZVHx48nrPimFdV1U1V9fGq+v5jeQIAAADjYi33wD2Y5Gdbax+qqlOTfLCq3jF4\n7bWttdes3Lmqzk3yoiRPSvKEJO+sqm9prR3cysIBAADGzVGvwLXWbm+tfWjw/J4kS0nOWOWQ85Nc\n3Vq7v7X2T0luSvK0rSgWAABgnK1rFcqq2pHkvCTvS/KMJBdX1UuTfCDLV+k+l+Vw994Vh92aIwS+\nqrowyYVJsn379iwuLq6/+h4bt/MdJwcOHNDfEaW3o01/R5fejjb9HW16+9XWHOCq6pQkf5nkp1tr\nX6iq1yf51SRt8OtvJvmJtb5fa+3KJFcmya5du9rk5OQ6yu65667NWJ3vmFlcXNTfEaW3o01/R5fe\njjb9HWH+zXxEa1qFsqpOzHJ4+9PW2puSpLV2Z2vtYGvty0n+IF+ZJnlbkrNWHH7mYBsAAACbsJZV\nKCvJXJKl1tpvrdh++ordXpDko4Pn1yR5UVU9oqq+Mck5Sd6/dSUDAACMp7VMoXxGkh9N8pGq+vBg\n288nmaqqp2Z5CuXNSX4qSVprH6uqNya5McsrWF5kBUoAAIDNO2qAa63tT1JHeOltqxwzm2R2E3UB\nAABwmDXdAwcAAED3BDgAAICeEOAAAAB6QoADAADoCQEOAACgJwQ4AACAnhDgAAAAekKAAwAA6AkB\nDgAAoCcEOAAAgJ4Q4AAAAHpCgAMAAOiJbV0XAMejqups7NZaZ2MDAHB8cwUOjqC1tuHH2Ze+dVPH\nAwDAwxHgAAAAekKAAwAA6AkBDgAAoCcEOAAAgJ4Q4AAAAHpCgAMAAOgJAQ4AAKAnBDgAAICeEOAA\njmJ+fj47d+7M3r17s3PnzszPz3ddEgAwprZ1XQDA8Wx+fj4zMzOZm5vLwYMHc8IJJ2R6ejpJMjU1\n1XF1AMC4EeAAVjE7O5sXv/jFueSSS7K0tJSJiYm8+MUvzuzsrAAHAAydAAewihtvvDH33nvvV12B\nu/nmm7suDQAYQ+6BA1jFSSedlIsvvjh79uzJtm3bsmfPnlx88cU56aSTui4NABhDrsABrOJLX/pS\nXve61+W8887LwYMHs7CwkNe97nX50pe+1HVpAMAYEuAAVnHuuefm+c9//kPugXvJS16SN7/5zV2X\nxhFUVWdjt9Y6GxuA8SHAAaxiZmbmiKtQzs7Odl0aR7CZELVj37W5+YrnbmE1ALD1BDiAVRxaaXLl\nFTgrUAIAXRHgAI5iamoqU1NTWVxczOTkZNflAABjzCqUAAAAPeEKHDBWLHIBAPSZK3DAWGmtbfhx\n9qVv3dTxAACbJcABAAD0hAAHAADQEwIcAABATwhwAAAAPSHAAQAA9MRRA1xVnVVVC1V1Y1V9rKpe\nMdj+2Kp6R1V9YvDrYwbbq6p+p6puqqobquo7jvVJAAAAjIO1XIF7MMnPttbOTfL0JBdV1blJ9iV5\nV2vtnCTvGnydJD+Q5JzB48Ikr9/yqgEAAMbQUQNca+321tqHBs/vSbKU5Iwk5ye5arDbVUmeP3h+\nfpI3tGXvTfLoqjp9yysHAAAYM+u6B66qdiQ5L8n7kmxvrd0+eOmOJNsHz89I8qkVh9062AYAAMAm\nbFvrjlV1SpK/TPLTrbUvVNW/v9Zaa1XV1jNwVV2Y5SmW2b59exYXF9dzeO+N2/mOG/0dXXo72vR3\nNB04cEBvR5j+jja9/WprCnBVdWKWw9ufttbeNNh8Z1Wd3lq7fTBF8q7B9tuSnLXi8DMH2x6itXZl\nkiuTZNeuXW1ycnJjZ9B
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa782d78e10>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"bp_data.plot(title=\"Total de points\",\n",
" kind=\"box\",\n",
" grid=True,\n",
" figsize=(15,5))"
]
},
{
"cell_type": "code",
"execution_count": 21,
"metadata": {
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [
{
"data": {
"text/plain": [
"Index(['301', '302', '303', '304', '309', '310', '311'], dtype='object', name='Classe')"
]
},
"execution_count": 21,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"df[[\"total\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).columns.droplevel()"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Français"
]
},
{
"cell_type": "code",
"execution_count": 22,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78276c1d0>"
]
},
"execution_count": 22,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHWJJREFUeJzt3X2QZWldH/Dvz+ldWXaXBYGMhAVmE1GbGsXASKJ0mW7H\nKGZNVitE6CJksdraSkVH1FjZ0U4FLauTWVMBN4UvtWVHtyzSi0EU3NEVgt2S9gXdhUVeGsKKC4Es\nLyayMlurMOOTP/rM0jP0Tvf22z333s+n6tbce+4553lu/6bvzPec5zynWmsBAACgP75k0B0AAADg\nQoIaAABAzwhqAAAAPSOoAQAA9IygBgAA0DOCGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzEwfZ2FOe\n8pR25MiRg2xyoB566KFceeWVg+4G+0BtR5v6ji61HW3qO7rUdrSNW33vueeeP2+tPXWr9Q40qB05\nciR33333QTY5UCsrK5menh50N9gHajva1Hd0qe1oU9/RpbajbdzqW1Uf2c56hj4CAAD0jKAGAADQ\nM4IaAABAzwhqAAAAPSOoAQAA9IygBgAA0DOCGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzE4PuAAAA\nMNyqamBtt9YG1vZ+ckYNAADYldbajh/PuvnOXW0/qgQ1AACAnhHUAAAAekZQAwAA6BlBDQAAoGcE\nNQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlADAADoGUENAACgZwQ1AACAnhHU\nAAAAekZQAwAA6BlBDQAAoGcENQAAgJ4R1AAAAHpmW0Gtqn6oqt5XVe+tqqWqelxVXVdV76iq+6rq\n9VV1+X53FgAAYBxsGdSq6ulJfiDJsdba0SSHkrw0yS1JXtNa+4okf5Fkbj87CgAAMC62O/RxIskV\nVTWR5PFJHkjyzUne0L1/e5Lv3PvuAQAAjJ9qrW29UtUrkywkeTjJW5K8MskfdmfTUlXPSPJb3Rm3\ni7e9KclNSXL48OHn33HHHXvX+547c+ZMrrrqqkF3g32gtqNNfUeX2o429R1dajvaXnHXQ/mlF105\n6G4cmJmZmXtaa8e2Wm9iqxWq6klJbkhyXZLPJPnvSV603Y601m5LcluSHDt2rE1PT29306G3srKS\ncfq840RtR5v6ji61HW3qO7rUdsTddVp9N7GdoY/fkuTPWmufbq19Pskbk7wwyRO7oZBJcm2Sj+9T\nHwEAAMbKdoLaR5P8g6p6fFVVkuNJ3p9kOcmLu3VuTPKm/ekiAADAeNkyqLXW3pH1SUPemeQ93Ta3\nJbk5yQ9X1X1JnpxkcR/7CQAAMDa2vEYtSVprr0ryqosWfzjJC/a8RwAAAGNuu9PzAwAAcEAENQAA\ngJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlDbB0tLSzl69GiOHz+eo0ePZmlpadBd\nAhgZVbXjx8zMzK62B4CDsq0bXrN9S0tLmZ+fz+LiYs6dO5dDhw5lbm4uSTI7Ozvg3gEMv9bajrc9\ncvJ07j91/R72BgD2hzNqe2xhYSGLi4uZmZnJxMREZmZmsri4mIWFhUF3DcaKsy4AwDAT1PbY2tpa\npqamLlg2NTWVtbW1AfUIxlNrbcePZ9185662BwDYLUFtj01OTmZ1dfWCZaurq5mcnBxQjwAAgGEj\nqO2x+fn5zM3NZXl5OWfPns3y8nLm5uYyPz8/6K4BAABDwmQie+z8hCEnTpzI2tpaJicns7CwYCIR\nAABg2wS1fTA7O5vZ2dmsrKxkenp60N0BAACGjKGPAAAAPSOoAQAA9IygBgAA0DOCGgAAQM8IagAA\nAD0jqAEAAPSMoAYAANAzghoAAEDPuOE1Y6uqBtZ2a21gbQMA0H/OqDG2Wms7fjzr5jt3tT0AAFyK\noAYAANAzghoAAEDPCGoAAAA9I6gBAAD0jKAGAADQM4IaAABAzwhqAAAAPSOoAQAA9IygBgAA0DOC\nGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzghoAAEDPCGoAwFBbWlrK0aNHc/z48Rw9ejRLS0uD7hLA\nrk0MugN9V1UDa7u1NrC2AWAYLC0tZX5+PouLizl37lwOHTqUubm5JMns7OyAewewc86obaG1tuPH\ns26+c1fbAwCXtrCwkMXFxczMzGRiYiIzMzNZXFzMwsLCoLsGsCuCGgAwtNbW1jI1NXXBsqmpqayt\nrQ2oRwB7w9BHAGBoTU5OZnV1NTMzM48sW11dzeTk5AB7xaMZ1CUlRioxjAQ1AGBozc/P5yUveUmu\nvPLKfPSjH80zn/nMPPTQQ7n11lsH3TU2sdPAdOTk6dx/6vo97g30m6AG9NZzf+ItefDhzw+k7SMn\nTx94m9dccVne/apvPfB2YVQ4awKMEkEN6K0HH/78QI6grqysZHp6+sDbHUQ4hGG3sLCQ17/+9ZmZ\nmXnkd3d5eTknTpww6yMw1EwmAgAMLZOJAKNKUAMAhtb5yUQ2MpkIMAq2FdSq6olV9Yaq+kBVrVXV\nN1TVl1XVW6vqQ92fT9rvzgIAbDQ/P5+5ubksLy/n7NmzWV5eztzcXObn5wfdNYBd2e41arcmuau1\n9uKqujzJ45P8WJK3tdZOVdXJJCeT3LxP/QQA+CLnr0M7ceJE1tbWMjk5mYWFBdenAUNvy6BWVdck\n+aYkr0iS1trnknyuqm5IMt2tdnuSlQhqAMABm52dzezs7MAmAgLYD9s5o3Zdkk8n+cWqem6Se5K8\nMsnh1toD3TqfSHJ4s42r6qYkNyXJ4cOHs7Kysts+D5Vx+7zjRG0PxiB+zmfOnBlYff292n9+xqNr\nkL+77D+1HW3q+8W2E9QmkjwvyYnW2juq6tasD3N8RGutVdWmNy9prd2W5LYkOXbsWBurI113nXZk\nb1Sp7cEY0M95YEfl/b3af37GI80ZtRHmd3e0qe+mthPUPpbkY621d3Sv35D1oPbJqnpaa+2Bqnpa\nkk/tVycBGC1uZg4Al7ZlUGutfaKq/ndVfVVr7YNJjid5f/e4Mcmp7s837WtPARgZbmYOAJe23Vkf\nTyR5XTfj44eTfE/Wp/b/laqaS/KRJN+9P10EAMZFVQ2s7dY2vYoDYCC2FdRaa/cmObbJW8f3tjsA\nwDjbTVg6cvL0QM7UAuyHbd3wGgAAgIMjqAEAAPSMoAYAANAzghoAAEDPCGoAAAA9s93p+YeaG6sC\nAADDZCyCmhurAgAAw2QsghoAAHBpRqH1i6AGAAAYhdYzJhMBAADoGWfUGGpO0QMAMIoENYaaU/QA\nAIwiQx8BAAB6RlADAADoGUENAACgZ1yjBvTW1ZMn8zW3nxxM47cffJNXTybJwV9zCQD0j6AG9NZn\n106ZLAYAGEuGPgIAAPSMM2oMNUPjAAAYRYIaQ83QOAAARpGhjwAAAD0jqAEAAPSMoAYAANAzY3GN\nmgknAACAYTIWQc2EEwAAwDAx9BEAAKBnxuKMGjC8BnaG+K6Db/eaKy478DYHxZB0ALg0QQ3orUEM\nWU7Ww+Gg2h4XhqQDwKUZ+ggAANAzghoAAEDPCGoAAAA9I6gBAAD0jKAGAADQM4IaAABAzwhqAAAA\nPeM+agAAQK6ePJmvuf3kYBq//eCbvHoySfp731RBDQAAyGfXTuX+UwcfXFZWVjI9PX3g7R45efrA\n23wsxiaoDawQdx18u9dccdmBtwkAAOydsQhqgzgykKyHw0G1DQCwH577E2/Jgw9//sDbHcRB92uu\nuCzvftW3Hni7kIxJUAMAYG88+PDnD/xAtKFxjCOzPgIAAPSMoAYAANAzhj4y9EwUAwDAqBHUGGom\nigEAYBQZ+ggAANAzghoAAEDPCGoAAAA94xo1AGBPDeqGyImbIgOjY9tBraoOJbk7ycdba99RVdcl\nuSPJk5Pck+TlrbXP7U83ARg1ZmwdXYO4IXLipsjAaHksZ9RemWQtyRO617ckeU1r7Y6q+vkkc0l+\nbo/7B8AIMmMrAFzatq5
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa7821912b0>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"Français\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Histoire géo"
]
},
{
"cell_type": "code",
"execution_count": 23,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa782063710>"
]
},
"execution_count": 23,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGD9JREFUeJzt3X+wpXddH/D3x2SBNAlBwVmQ0CwtVJMWgrJFLG3nBjVF\n4xQ6tVZGMVo6mVaZ+qNWbuu0KWOdbqb4qy1DJ1MYV4cxOqgDk2VCKt1bbKuOBIkCEYk0jAE0tZIf\nm2YgyKd/3LNy2e5yz/11nu895/WaObP3POd5zud77ufcc+97n+/5nuruAAAAMI4vmnoAAAAAfD5B\nDQAAYDCCGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEAAAxGUAMAABiMoAYAADCYixdZ7GlPe1of\nO3ZskSUn9eijj+bSSy+dehgcAL1dbvq7vPR2uenv8tLb5bZq/b3rrrv+uLu/dLv9FhrUjh07lve8\n5z2LLDmpjY2NrK2tTT0MDoDeLjf9XV56u9z0d3np7XJbtf5W1Ufn2c/URwAAgMEIagAAAIMR1AAA\nAAYjqAEAAAxGUAMAABiMoAYAADAYQQ0AAGAwghoAAMBgBDUAAIDBCGoAAACDuXjqAYyuqiar3d2T\n1V4FegsAwKicUdtGd+/6ctVrb9/T8RwsvQUAYFSCGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEA\nAAxGUAMAABiMoAYAADAYQQ0AAGAwghoAAMBgBDUAAIDBCGoAAACDEdQAAAAGM3dQq6qLquq3qur2\n2fVnV9VvVNW9VfXzVfWEgxsmAADA6tjJGbXvTXLPluu3JPmJ7n5Okk8mefV+DgwAAGBVzRXUqurK\nJDck+c+z65XkpUneOtvlZJJXHMQAAQAAVs28Z9R+MskPJfns7PpTkzzY3Z+ZXb8/yTP3eWwAAAAr\n6eLtdqiqb0ryQHffVVVrOy1QVTcluSlJjh49mo2NjZ3exaG2ao93lejt8jpz5oz+Lim9XW76u7z0\ndrnp7/ltG9SSvCTJ366qb0zypCRPTvJTSZ5SVRfPzqpdmeRj5zu4u29NcmuSHD9+vNfW1vZj3IfD\nHaeyUo93lejtUtvY2NDfJaW3y01/l5feLjf9Pb9tpz529z/v7iu7+1iSb03yX7v725KcTvLNs91u\nTPK2AxslAADACtnL56i9NskPVNW92XzP2pv2Z0gAAACrbZ6pj3+muzeSbMy+/kiSF+3/kAAAAFbb\njoIaAExt8xNiptHdk9UGYLXsZeojACxcd+/6ctVrb9/T8QCwKIIaAADAYAQ1AACAwQhqAAAAgxHU\nAAAABiOoAQAADEZQAwAAGIygBgAAMBhBDQAAYDCCGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEA\nAAxGUAMAABiMoAYAADAYQQ0AAGAwF089gEW49nV35qHHHp+k9rH1UwuvecUlR3L3zdcvvC4AALA/\nViKoPfTY47nvxA0Lr7uxsZG1tbWF150iHAIAAPvH1EcAAIDBCGoAAACDEdQAAAAGI6gBAAAMRlAD\nAAAYjKAGAAAwGEENAABgMIIaAADAYAQ1AACAwQhqAAAAgxHUAAAABnPx1AOAvbj2dXfmoccen6T2\nsfVTC695xSVHcvfN1y+8LgAAiyWocag99Njjue/EDQuvu7GxkbW1tYXXnSIcAgCweKY+AgAADEZQ\nAwAAGMxKTH28/Or1PO/k+jTFTy6+5OVXJ8nipwPCSKpqstrdPVltAGA5rERQe+SeE97HBCtmL2Hp\n2PqpSV4zAADOMvURAABgMIIaAADAYAQ1AACAwQhqAAAAg1mJxUQAAJjeVCvyWo2Xw8gZNQAAFqK7\nd3W56rW37/pYIY3DSlADAAAYjKAGAAAwGEENAABgMIIaAADAYAQ1AACAwVieH4CFu/Z1d+ahxx6f\npPax9VMLr3nFJUdy983XL7wuAIfXtkGtqp6U5N1Jnjjb/63dfXNVPTvJbUmemuSuJK/q7k8f5GAB\nWA4PPfZ47jtxw8LrbmxsZG1tbeF1pwiHABxu80x9/FSSl3b3tUlekORlVfXiJLck+Ynufk6STyZ5\n9cENEwAAYHVsG9R605nZ1SOzSyd5aZK3zrafTPKKAxkhAADAipnrPWpVdVE2pzc+J8kbkvx+kge7\n+zOzXe5P8swLHHtTkpuS5OjRo9nY2NjjkHdnirpnzpxZqcc7Fb3lIPg+Hzw/u+y3KfvLwdPb5eVn\n9/zmCmrd/adJXlBVT0nyy0m+Yt4C3X1rkluT5Pjx4z3FewNyx6lJ3pMw1Xshpnq8k9BbDoLv88Hz\ns8sBmKy/HDw/Q0vNz+757Wh5/u5+MMnpJF+T5ClVdTboXZnkY/s8NgAAgJW0bVCrqi+dnUlLVV2S\n5OuT3JPNwPbNs91uTPK2gxokAADAKpln6uMzkpycvU/ti5L8QnffXlUfTHJbVf2bJL+V5E0HOE4A\nAICVsW1Q6+7fTvKV59n+kSQvOohBAQAArLK5FhMBAAC4kKqarHZ3T1b7IO1oMREAAIBzdfeuL1e9\n9vY9Hb+sBDUAAIDBCGoAAACDEdQAAAAGI6gBAAAMRlADAAAYjKAGAAAwGJ+jBsDCXX71ep53cn2a\n4icXX/Lyq5PkhsUXBuDQEtQAWLhH7jmR+04sPrhsbGxkbW1t4XWPrZ9aeE0ADjdTHwEAAAbjjBoA\nMIyqmqx2d09WG+BczqgBAMPo7l1frnrt7Xs6HmAkghoAAMBgTH3kULNyHAAAy0hQ41CzchwAAMvI\n1EcAAIDBCGoAAACDMfURGNa1r7szDz32+CS1p5hmesUlR3L3zdcvvC4AMB5BDRjWQ4897j2IAMBK\nMvURAABgMIIaAADAYAQ1AACAwXiPGgAAc5tqoSeLPLFqBDUAAOY2xUJPFnliFZn6CAAAMBhBDQAA\nYDCmPnLoTTYt4Y5p5soDALD8BDUOtSk+DDnZDIdT1QYAYPmZ+ggAADAYQQ0AAGAwghoAAMBgBDUA\nAIDBCGoAAACDWZlVHy3hDgAAHBYrEdQs4Q4AABwmpj4CAAAMRlADAAAYjKAGAAAwmJV4jxoAAPCF\nXfu6O/PQY49PUnuKhf+uuORI7r75+oXXnZegBgAA5KHHHp9kIbyNjY2sra0tvO5kq8LPydRHAACA\nwQhqAAAAgzH1ERjW5Vev53kn16cpfnLxJS+/Okl89iIAIKgBA3vknhPmygMAK8nURwAAgME4owbA\nJCY7g3jHNEtAA8BOCGoALNwUU1qTzXA4VW0A2Iltpz5W1bOq6nRVfbCqPlBV3zvb/iVV9V+q6sOz\nf7/44IcLAACw/OZ5j9pnkvzT7r4myYuTfE9VXZNkPcm7uvu5Sd41uw4AAMAebRvUuvsT3f3e2deP\nJLknyTOTvDyfW8D6ZJJXHNQgAQAAVsmOVn2sqmNJvjLJbyQ52t2fmN30h0mO7uvIAAAAVtTci4lU\n1WVJfjHJ93X3w1X1Z7d1d1dVX+C4m5LclCRHjx7NxsbGngZ82Kza410lersYU3yfz5w5M1l/Pa8O\nnu/xwfuedz2aRx+fpvYUq4leeiR5w9deuvC6U1r0z5HX5cXxe3cccwW1qjqSzZD2lu7+pdnmP6qq\nZ3T3J6rqGUkeON+x3X1rkluT5Pjx4z3Fh8hO5o5Tk3xoLgugt4sx0fd5qg+89rxaAN/jhXj0jmlW\n15zyw+pX6nk1wc+R1+UF8Xt3KPOs+lhJ3pTknu7+8S03vT3JjbOvb0zytv0fHgAAwOqZ54zaS5K8\nKsnvVNX7Ztv+RZITSX6hql6d5KNJvuVghggAALBatg1q3f3fk9QFbv7a/R0OAAAAO1r1EQAAgIMn\nqAEAAAxGUAMAABiMoAYAADAYQQ0AAGAwghoAAMBg5vkctZW2+Xnfezj+lt0f2917qg0AABxOzqht\no7t3fTl9+vSejgcAAFaToAYAADAYQQ0AAGAwghoAAMBgBDUAAIDBWPWRlWVFTwCAz7n86vU87+T6\nNMVPLr7k5VcnyQ2LLzw
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa782038160>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"HG\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Les maths"
]
},
{
"cell_type": "code",
"execution_count": 24,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa781ed5b70>"
]
},
"execution_count": 24,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHhdJREFUeJzt3X2QZWddJ/DvzxmCkYQXwRqRIMOWrHYcQGAKEWatbkcp\n2LgLW4tKRzRCr1nLZUR8Y3a7dpFyuyqp1VXWWFpZO0tUqqOyLrAEQjR2L0yhFC+CBNqXLCa8GERr\nJTCYIpnh2T/6DnTGSboz3X3Pued+PlVd0/fcc/r5df96bve3z3OeU621AAAA0B9f0XUBAAAA3Jeg\nBgAA0DOCGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzghoAAEDPCGoAAAA9I6gBAAD0zP5xDvaYxzym\nHTx4cJxDdurzn/98Hvawh3VdBntAb4dNf4dLb4dNf4dLb4dt2vr7vve97+9aa1+z1X5jDWoHDx7M\ne9/73nEO2am1tbXMzs52XQZ7QG+HTX+HS2+HTX+HS2+Hbdr6W1V3bGc/Ux8BAAB6RlADAADoGUEN\nAACgZwQ1AACAnhHUAAAAekZQAwAA6BlBDQAAoGcENQAGb2VlJYcOHcrRo0dz6NChrKysdF0SwNTz\n2vzAxnrDawAYt5WVlSwuLmZ5eTmnT5/Ovn37srCwkCSZn5/vuDqA6eS1eWvOqAEwaEtLS1leXs7c\n3Fz279+fubm5LC8vZ2lpqevSAKaW1+atCWp7wGlcgP5YX1/PkSNH7rPtyJEjWV9f76giALw2b83U\nx13mNC5Av8zMzOTEiROZm5v70rYTJ05kZmamw6oAppvX5q05o7bLnMYF6JfFxcUsLCxkdXU1p06d\nyurqahYWFrK4uNh1aQBTy2vz1pxR22VO4wL0y5nZDMeOHcv6+npmZmaytLRklgNAh7w2b80ZtV12\n5jTuZk7jAnRrfn4+t956a2655ZbceuutfhEA6AGvzQ9MUNtlTuMCAAA7ZerjLnMaFwAA2ClBbQ/M\nz89nfn4+a2trmZ2d7bocAABgwpj6CAAA0DOCGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzghoAAEDP\nCGoAAAA9I6gBAAD0jKAGAADQM4IaAABAzwhqAAAAPSOoAQAA9IygBgAA0DOCGgAAQM8IagAAAD0j\nqAEAAPSMoAYAANAz2wpqVfXKqvpwVd1aVStV9ZVV9cSqendV3VZVv11VF+x1sQAAANNgy6BWVY9L\n8mNJDrfWDiXZl+TFSa5O8outtW9I8vdJFvayUAAAgGmx3amP+5NcWFX7k3xVkjuTfEeSN4yevz7J\nC3e/PAAAgOlTrbWtd6p6RZKlJHcnuTnJK5L88ehsWqrq8UneNjrjdvaxVya5MkkOHDjwjBtuuGH3\nqu+5kydP5qKLLuq6DPaA3g6b/g6X3g6b/g6X3vbf3NxcZ2Ovrq52Nvb5mJube19r7fBW++3faoeq\nelSSFyR5YpLPJPndJM/bbiGttWuTXJskhw8fbrOzs9s9dOKtra1lmj7faaK3w6a/w6W3w6a/w6W3\n/bedkz/35+DxG3P7VZftYjXDsJ2pj9+Z5K9aa3/bWrs3ye8leU6SR46mQibJJUk+uUc1AgAATJXt\nBLWPJXlWVX1VVVWSo0k+kmQ1yYtG+1yR5E17UyIAAMB02TKotdbenY1FQ96f5EOjY65N8qokP1FV\ntyV5dJLlPawTAABgamx5jVqStNZeneTVZ23+aJJn7npFAAAAU267y/MDAAAwJoIaAABAz2xr6iPA\npNlY+6gbO1miGAAgcUYNGKjW2nm/PeFVb9nR8QAAOyWoAQAA9IygtgdWVlZy6NChHD16NIcOHcrK\nykrXJQEAABPENWq7bGVlJYuLi1leXs7p06ezb9++LCwsJEnm5+c7rg4AAJgEzqjtsqWlpSwvL2du\nbi779+/P3NxclpeXs7S01HVpAADAhBDUdtn6+nqOHDlyn21HjhzJ+vp6RxUBAACTRlDbZTMzMzlx\n4sR9tp04cSIzMzMdVQQAAEwaQW2XLS4uZmFhIaurqzl16lRWV1ezsLCQxcXFrksDAAAmhMVEdtmZ\nBUOOHTuW9fX1zMzMZGlpyUIiAADAtglqe2B+fj7z8/NZW1vL7Oxs1+UAAAATxtRHAACAnhHUAAAA\nekZQAwAA6BnXqDG1qqqzsVtrnY0NAED/OaPG1GqtnffbE171lh0dDwAAD0RQAwAA6BlBDQAAoGcE\nNQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlADAADoGUENAACgZwQ1AACAnhHU\nAAAAekZQAwAA6BlBDQAAoGcENQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlAD\nAADoGUENAACgZwQ1AACAnhHUAAAAekZQAwAA6Jn9XRcAO/HU19ycu+6+t5OxDx6/cexjPuLCh+SD\nr37u2McFAGC8BLUtVFVnY7fWOht7Utx19725/arLxj7u2tpaZmdnxz5uF+EQAIDxM/VxC6218357\nwqvesqPjAQCA6bStoFZVj6yqN1TVn1XVelV9W1V9dVX9flX95ejfR+11sQAAANNgu2fUXpvkptba\nNyV5apL1JMeT3NJae1KSW0aPAQAA2KEtg1pVPSLJtydZTpLW2j2ttc8keUGS60e7XZ/khXtVJAAA\nwDTZzhm1Jyb52yT/o6r+pKp+vaoeluRAa+3O0T6fSnJgr4oEAACYJttZ9XF/kqcnOdZae3dVvTZn\nTXNsrbWqOufqF1V1ZZIrk+TAgQNZW1vbWcUTZto+3y508TU+efJkZ731PTUevs7D1OX/Xfae/g6X\n3g6f/v5j2wlqn0jyidbau0eP35CNoPY3VfXY1tqdVfXYJJ8+18GttWuTXJskhw8fbl0sad6Zm27s\nZAn3qdLR17ir5fl9T42Jr/NgdfZ/l7HQ3+HS24Hzc/ectpz62Fr7VJKPV9U3jjYdTfKRJG9OcsVo\n2xVJ3rQnFQIAAEyZ7d7w+liS11fVBUk+muSl2Qh5v1NVC0nuSPK9e1MiAADAdNlWUGutfSDJ4XM8\ndXR3ywEAAGC791EDAABgTAQ1AACAnhHUAAAAekZQAwAA6BlBDQAAoGcENQAAgJ4R1AAAAHpGUAMA\nAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlADAADoGUENAACgZwQ1AACAnhHUAAAAekZQAwAA6BlBDQAA\noGcENQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICe2d91AePw1NfcnLvuvreTsQ8ev3HsYz7i\nwofkg69+7tjHBYAurKysZGlpKevr65mZmcni4mLm5+e7LgtgR6YiqN119725/arLxj7u2tpaZmdn\nxz5uF+EQALqwsrKSxcXFLC8v5/Tp09m3b18WFhaSRFgDJpqpjwDAxFpaWsry8nLm5uayf//+zM3N\nZXl5OUtLS12XBrAjghoAMLHW19dz5MiR+2w7cuRI1tfXO6oIYHcIagDAxJqZmcmJEyfus+3EiROZ\nmZnpqCKA3SGoAQATa3FxMQsLC1ldXc2pU6eyurqahYWFLC4udl0awI5MxWIiAMAwzc/P513velee\n//zn5wtf+EIe+tCH5od/+IctJAJMPEENAJhYKysrufHGG/O2t73tPqs+PvvZzxbWgIlm6iMAMLGs\n+ggMlaAGAEwsqz4CQyWoAQATy6qPwFC5Rg3orae+5ubcdfe9nYx98PiNYx/zERc+JB989XPHPi5M\nsjOrPi4vL+f06dNfWvXR1Edg0glqQG/ddfe9uf2qy8Y+7traWmZnZ8c+bhfhECbdmQVDjh07lvX1\n9czMzGRpaclCIsDEE9QAgIk2Pz+f+fn5zv7IArAXBDUm2sUzx/Pk6493M/j14x/y4pkkGf8ZJgAA\nxktQY6J9bv0qU+MAABgcqz4CAAD0jKAGAADQM6Y+AgAAbovTM4IaAADgtjg9Y+ojABOlqs77bW5u\nbkfHA+O1srKSQ4cO5ej
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa781f20748>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"Maths\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## SVT"
]
},
{
"cell_type": "code",
"execution_count": 25,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa781e9dcc0>"
]
},
"execution_count": 25,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGORJREFUeJzt3X2MpVd9H/DvD3YDG3Adg8PWvJSlCk2WmBrChlSN287W\n4KBYBFBpmhWiTrBqogREIKnYYKnGQY7WVQN9QWpjtBCnShdSXgr1BteuMxPipkWxKQbDRoGmi4pr\ncF2SxUu36dqc/jGPYVjP7ozn5T7n3vv5SFd753k7Z+5v7t35znOe81RrLQAAAPTjcWN3AAAAgO8k\nqAEAAHRGUAMAAOiMoAYAANAZQQ0AAKAzghoAAEBnBDUAAIDOCGoAAACdEdQAAAA6s2OSjV144YVt\nz549k2xyVN/4xjfypCc9aexusA3Udrap7+xS29mmvrNNfWfXvNX2rrvueqC19r1rbTfRoLZnz57c\neeedk2xyVEtLS1lYWBi7G2wDtZ1t6ju71Ha2qe9sU9/ZNW+1raovrWc7Qx8BAAA6I6gBAAB0RlAD\nAADojKAGAADQGUENAACgM4IaAABAZwQ1AACAzqwZ1KrqWVW1WFWfr6rPVdWbhuVvr6p7q+rTw+PH\nt7+7AAAAs289N7x+KMkvttY+VVXnJbmrqm4b1r2rtfZPtq97AAAA82fNoNZauy/JfcPzB6vqWJJn\nbHfHAAAA5lW11ta/cdWeJJ9IcnGStyT56SRfT3Jnls+6/ekq+1yd5Ook2b1794ve//73b7bPE7V/\n//7R2l5cXBytbc7t5MmTefKTnzx2N9gm6ju71Ha2qe9sU9+++Z15/fbv339Xa23fWtutO6hV1ZOT\n/F6S61trH66q3UkeSNKSvCPJRa21153rGPv27Wt33nnnutqbBXsOHs3xQ1eM3Q22wdLSUhYWFsbu\nBttEfWeX2s429Z1t6ju75u135qpaV1Bb16yPVbUzyYeS/FZr7cNJ0lr7amvt4dbaN5O8J8mLN9Nh\nAAAAlq1n1sdKcjjJsdbaO1csv2jFZq9Kcs/Wdw8AAGD+rGfWxx9N8tokn62qTw/L3pbkQFW9IMtD\nH48nef229BAAAGDOrGfWxzuS1CqrfmfruwMAAMC6rlEDAABgcgQ1AACAzghqAAAAnRHUAAAAOiOo\nAQAAdEZQAwAA6IygBgAA0BlBDQAAoDOCGgAAQGcENQAAgM4IagAAAJ0R1AAAADojqAEAAHRGUAMY\nHDlyJBdffHEuu+yyXHzxxTly5MjYXQIA5tSOsTsA0IMjR47kmmuuyeHDh/Pwww/n8Y9/fK666qok\nyYEDB0buHQAwb5xRA0hy/fXX5/Dhw9m/f3927NiR/fv35/Dhw7n++uvH7hoAMIecUWNuVdVobbfW\nRmub1R07diyXXnrpdyy79NJLc+zYsZF6BADMM2fUmFuttQ0/nv3Wmze1P/3Zu3dv7rjjju9Ydscd\nd2Tv3r0j9QgAmGeCGkCSa665JldddVUWFxfz0EMPZXFxMVdddVWuueaasbsGAMwhQx8B8u0JQ974\nxjfm2LFj2bt3b66//noTiQAAoxDUAAYHDhzIgQMHsrS0lIWFhbG7AwDMMUMfAQAAOiOoAQAAdEZQ\nAwAA6IygBgAA0BlBDQAAoDOCGgAAQGcENQAAgM4IagAAAJ0R1AAAADojqAEAAHRGUAMAAOiMoAYA\nANAZQQ0AAKAzghoAAEBnBDUAAIDOCGoAAACdEdQAAAA6I6gBAAB0ZsfYHYDNuOS6W3Pi1OlR2t5z\n8OjE2zx/187cfe3lE28XAIDJEtSYaidOnc7xQ1dMvN2lpaUsLCxMvN0xwiEAAJNn6CMAAEBnBDUA\nAIDOCGoAAACdEdQAAAA6s2ZQq6pnVdViVX2+qj5XVW8alj+lqm6rqi8M/16w/d0FAACYfes5o/ZQ\nkl9srT0vyV9L8vNV9bwkB5Pc3lp7bpLbh68BAADYpDWDWmvtvtbap4bnDyY5luQZSV6R5KZhs5uS\nvHK7OgkAADBPHtN91KpqT5IXJvlkkt2ttfuGVV9Jsvss+1yd5Ook2b17d5aWljbY1ek0b9/vGMZ4\njU+ePDlabf1Mbb8x68v2UtvZpr6zTX1nm9o+2rqDWlU9OcmHkvxCa+3rVfWtda21VlVttf1aazcm\nuTFJ9u3b18a4SfBobjk6yk2R58pIr/FYN7z2MzUZo9WXbae2s019Z5v6zjC/36xqXbM+VtXOLIe0\n32qtfXhY/NWqumhYf1GS+7eniwAAAPNlPbM+VpLDSY611t65YtXHklw5PL8yyUe3vnsAAADzZz1D\nH380yWuTfLaqPj0se1uSQ0l+u6quSvKlJD+5PV0EAACYL2sGtdbaHUnqLKsv29ruAGyNldfRTlpr\nq16yyxYaq75qC8CkrOsaNYBp01rb8OPZb715U/uz/dQWgFknqAEAAHRGUAMAAOiMoAYAANAZQQ0A\nAKAzghoAAEBnBDUAAIDOCGoAAACdEdQAAAA6I6gBAAB0RlADAADojKAGAADQGUENAACgM4IaAABA\nZwQ1AACAzghqAAAAndkxdgcAAJgPVTVa26210dqGjXBGDQCAiWitbfjx7LfevKn9YdoIagAAAJ0R\n1AAAADojqAEAAHRmLiYTueS6W3Pi1OlR2t5z8OjE2zx/187cfe3lE28XAADYGnMR1E6cOp3jh66Y\neLtLS0tZWFiYeLtjhEMAAGDrGPoIAADQGUENAACgM4IaAABAZwQ1AACAzghqAAAAnZmLWR8BAIBz\nc0urvghqAACAW1p1xtBHAACAzghqAAAAnTH0kal23t6Def5NB8dp/KbJN3ne3iSZ/JAEAAAmS1Bj\nqj147JCx1AAAzBxDHwEAADojqAEAAHRGUAMAAOiMa9QAgG5U1Whtt9ZGaxvgTM6oAQDdaK1t+PHs\nt968qf0BeiKoAQAAdMbQRwBGccl1t+bEqdMTb3eM21ycv2tn7r728om3C8D0EtQAGMWJU6cnfh9E\n90AEYFoY+ggAANAZQQ0AAKAzawa1qnpvVd1fVfesWPb2qrq3qj49PH58e7sJAAAwP9ZzRu03krxs\nleXvaq29YHj8ztZ2CwAAYH6tGdRaa59I8rUJ9AUAAIBs7hq1N1TVZ4ahkRdsWY8AAADm3Ean5/+X\nSd6RpA3//lqS1622YVVdneTqJNm9e3eWlpY22OTmjNHuyZMn5+r7HYvash28zpMx6dfZe3f2eZ1n\nm/puP79X9WNDQa219tVHnlfVe5LcfI5tb0xyY5Ls27evjXH/mtxydJT75ox1v56xvt9RqC3bwes8\nGSO8zt67M87rPNvUd/v5vaorGxr6WFUXrfjyVUnuOdu2AAAAPDZrnlGrqiNJFpJcWFVfTnJtkoWq\nekGWhz4eT/L6bewjAADAXFkzqLXWDqyy+PA29AUAAIBsfDIRgG13yXW35sSp06O0vefg0Ym3ef6u\nnbn72ssn3i4A0B9BDejWiVOnc/zQFRNvd6yLmscIhwBAnzZzHzUAAAC2gaAGAADQGUENAACgM4Ia\nAABAZwQ1AACAzghqAAAAnRHUAAAAOiOoAQAAdMYNr5l6o90k+JbJt3v+rp0TbxMAgMkT1Jhqxw9d\nMUq7ew4eHa1tgN5dct2tOXHq9Chtj/HHu/N37czd114+8XaB2SaoAQBb6sSp06P8MWtpaSkLCwsT\nb3e0kR3ATHONGgAAQGcENQAAgM4IagAAAJ1xjRoAozhv78E8/6aDk2/4psk3ed7eJDEBEQDrJ6gB\nMIoHjx2a+IQTJpsAYFoY+ggAANAZQQ0AAKAzghoAAEBnBDUAAIDOzMVkIqPNLJaYXQwAAHjM5iKo\njTGzWGJ2MQAAYGMMfQQAAOiMoAYAANAZQQ0AAKAzghoAAEBnBDUAAIDOCGoAAACdmYvp+YHp5B6I\nADA5/t/ti6AGdMs9EAFgcvy/2xdDHwEAADojqAEAAHRGUAMAAOiMoAYAANAZQQ0AAKAzghoAAEBn\nTM8PAGwp92KabZdcd2t
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa781da3a58>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"SVT\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Physique"
]
},
{
"cell_type": "code",
"execution_count": 26,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa781bc8780>"
]
},
"execution_count": 26,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAG0lJREFUeJzt3X2MZeddH/DvL7sGjO28gGFrQpolNMBEGxLINgJlaWdY\nSC2sKlDR0BEvBkYyCOICChJTBjXQaKSNFKhoqQqOJmSThokKIYVmg3GwZjDb8hI7coiTARLopjgx\ncSOC4zUGvJunf9y7yex61zM7L/ece+/nI432zrnn3Oe5891zd79zzj23WmsBAACgP57W9QQAAAC4\nmKIGAADQM4oaAABAzyhqAAAAPaOoAQAA9IyiBgAA0DOKGgAAQM9sWdSq6jlVtVZVH6yqD1TVjwyX\n/3RVfbSq7h9+fcv+TxcAAGDy1VYfeF1VNyW5qbX23qq6Icl9Sb41ySuTnG2tvX7/pwkAADA9Dm61\nQmvtoSQPDW8/WlUbSZ69k8FuvPHGdvjw4Z1sOpYee+yxXHfddV1Pg30g28km38kl28km38km38k1\nbdned999n2itfdFW621Z1DarqsNJvibJHyZ5WZJXVdX3JLk3yatba5+8zDa3JbktSQ4dOpTXv356\nDsCdPXs2119/fdfTYB/IdrLJd3LJdrLJd7LJd3JNW7Zzc3Mf2c56W576+JkVq65P8rtJlltrv15V\nh5J8IklL8toMTo/8/qd6jKNHj7Z77713W+NNgvX19czOznY9DfaBbCebfCeXbCebfCebfCfXtGVb\nVfe11o5utd62rvpYVdckeXuSt7bWfj1JWmsfb62db619Oskbkrx0NxMGAABgYDtXfawkK0k2Wms/\nt2n5TZtW+7YkD+z99AAAAKbPdt6j9rIk353k/VV1/3DZTyaZr6oXZ3Dq45kkP7AvMwQAAJgy27nq\n4+kkdZm73rX30wEAAGBb71EDAABgdBQ1AACAnlHUAIZWV1dz5MiRHD9+PEeOHMnq6mrXUwIAptRV\nfeA1wKRaXV3N0tJSVlZWcv78+Rw4cCALCwtJkvn5+Y5nBwBMG0fUAJIsLy9nZWUlc3NzOXjwYObm\n5rKyspLl5eWupwYATCFFDSDJxsZGjh07dtGyY8eOZWNjo6MZAQDTTFEDSDIzM5PTp09ftOz06dOZ\nmZnpaEYAwDRT1ACSLC0tZWFhIWtrazl37lzW1taysLCQpaWlrqcGAEwhFxMByGcvGHL77bdnY2Mj\nMzMzWV5ediERAKATihrA0Pz8fObn57O+vp7Z2dmupwMATDGnPgIAAPSMogYAANAzihoAAEDPKGoA\nAAA9o6gBAAD0jKIGAADQM4oaAABAzyhqAAAAPaOoAQAA9IyiBgAA0DOKGgAAQM8oagAAAD2jqAEA\nAPSMogYAANAzihoAAEDPKGoAAAA9o6gBAAD0jKIGAADQMwe7ngAAXK2q6mTc1lon4wIwfRxRA2Ds\ntNZ29PXcn3jnjrdV0gAYJUUNAACgZxQ1AACAnlHUAAAAekZRAwAA6BlFDQAAoGcUNQAAgJ5R1ACA\nsba6upojR47k+PHjOXLkSFZXV7ueEsCu+cBrAGBsra6uZmlpKSsrKzl//nwOHDiQhYWFJMn8/HzH\nswPYOUfUAICxtby8nJWVlczNzeXgwYOZm5vLyspKlpeXu54awK4oagDA2NrY2MixY8cuWnbs2LFs\nbGx0NCOAvaGoAQBja2ZmJqdPn75o2enTpzMzM9PRjAD2hqIGAIytpaWlLCwsZG1tLefOncva2loW\nFhaytLTU9dQAdsXFRACAsXXhgiG33357NjY2MjMzk+XlZRcSAcaeogYAjLX5+fnMz89nfX09s7Oz\nXU8HYE849REAAKBnFDUAAICeUdQAAAB6ZsuiVlXPqaq1qvpgVX2gqn5kuPwLqurdVfWh4Z/P2v/p\nAgAATL7tHFE7l+TVrbUXJPm6JD9cVS9Ispjk7tba85PcPfweAACAXdqyqLXWHmqtvXd4+9EkG0me\nneQVSU4OVzuZ5Fv3a5IAAADTpFpr21+56nCSe5IcSfJ/W2vPHC6vJJ+88P0l29yW5LYkOXTo0Eve\n9ra37X7WY+Ls2bO5/vrru54GVzA3N9fZ2Gtra52Nzdbsu5Pre+98LG+6+bqup8E+se9ONvn2m/9X\nbd/c3Nx9rbWjW6237c9Rq6rrk7w9yY+21j416GYDrbVWVZdtfK21O5LckSRHjx5t0/T5Jj7Ppd+u\n5pcUlzq8eCpnTtyyh7OhT+y7E+zOU7KdYPbdySbffvP/qr23ras+VtU1GZS0t7bWfn24+ONVddPw\n/puSPLw/UwQAAJgu27nqYyVZSbLRWvu5TXf9ZpJbh7dvTfIbez89AACA6bOdUx9fluS7k7y/qu4f\nLvvJJCeS/PeqWkjykSSv3J8pAgAATJcti1pr7XSSusLdx/d2OgAAAGzrPWoAAACMjqIGAADQM4oa\nAABAzyhqAAAAPaOoAQAA9IyiBgAA0DPb+Ry1qTb4vO9utNY6GxvGnX0XABhnjqhtobW246/n/sQ7\nd7U9sHP2XQBgnClqAAAAPaOoAQAA9IyiBgAA0DOKGgAAQM8oagAAAD2jqAEAAPSMogYAANAzihoA\nAEDPKGoAAAA9o6gBAAD0jKIGAADQM4oaAABAzyhqAAAAPaOoAQAA9IyiBgAA0DOKGgAAQM8oagAA\nAD2jqAEAAPSMogYAANAzihoAAEDPKGoAAAA9o6gBAAD0jKIGAADQM4oaAABAzyhqAAAAPaOoAQAA\n9IyiBgAA0DOKGgAAQM8oagAAAD2jqAEAAPSMogYAANAzB7uewCi86GfuyiOPP9HJ2IcXT418zGdc\ne03e95qXj3zcLsgWYLJUVWdjt9Y6GxvgUlNR1B55/ImcOXHLyMddX1/P7OzsyMftokB0RbYAk2U3\nZenw4qlO/k0A2A9OfQQAAOgZRQ0AAKBnFDUAAICeUdQAAAB6RlEDAADoGUUNAACgZ7YsalX1xqp6\nuKoe2LTsp6vqo1V1//DrW/Z3mgAAANNjO0fU3pTk5sss/4+ttRcPv961t9MCAACYXlsWtdbaPUn+\negRzAQAAIMnBXWz7qqr6niT3Jnl1a+2Tl1upqm5LcluSHDp0KOvr67sYcue6GPfs2bNT9Xy7cMPM\nYl54crGbwU+OfsgbZpL19etGP/AUmpZ9aBrJdrLJt9/m5uY6G3ttba2zsdmafffJdlrU/muS1yZp\nwz9/Nsn3X27F1todSe5IkqNHj7bZ2dkdDrkLd55KF+Our693Mm5Xz7cLjy6eyJkTt4x83K6yPbx4\nKrO3jn7cqTNF+9DUke1kk2/vtdZ2vO3hxVOd/JvPCNh3L2tHV31srX28tXa+tfbpJG9I8tK9nRYA\nAMD02lFRq6qbNn37bUkeuNK6AAAAXJ0tT32sqtUks0lurKoHk7wmyWxVvTiDUx/PJPmBfZwjAADA\nVNmyqLXW5i+zeGUf5gIAAEB2eOojAAAA+0dRAwAA6BlFDQAAoGcUNQAAgJ5R1AAAAHpGUQMAAOgZ\nRQ0AAKBnFDUAAICe2fIDrwFgP7zoZ+7KI48/MfJxDy+eGvmYz7j2mrzvNS8f+bgAjC9FDYBOPPL4\nEzlz4paRjrm+vp7Z2dmRjpl0Uw4BGG9OfQQAAOgZRQ0AAKBnFDUAAICeUdQAAAB6RlEDAADoGUUN\nAACgZxQ1AACAnpmKz1G7YWYxLzy52M3gJ0c/5A0zSTLazybqUmefT3RnNx+aO026+kDkxIciAwDd\nmoqi9ujGiZF/qGrig1VHoYtck8HPuKuxp0kXH4ic2HcBgO459REAAKBnFDUAAICeUdQAAAB6RlED\nAADomam4mAgAAPDUXG25XxQ1AADA1ZZ7xqmPAAAAPaOoAQAA9IyiBgAA0DOKGgAAQM8oagAAAD2j\nqAEAAPSMogYAANAzihoAAEDPKGoAAAA9o6gBAAD0jKIGAADQM4oaAABAzyhqAAAAPaOoAQAA9MzB\nricwKocXT3Uz8J2jH/c
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa781c0ce48>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"Physique\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Techno"
]
},
{
"cell_type": "code",
"execution_count": 27,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa781a39ef0>"
]
},
"execution_count": 27,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGgJJREFUeJzt3X+QnddZH/Dvg+Q0xhiX1EQTEmqVENqlCkmpoBBU2K2D\nm9alBIbS2baQoTt1fxAVWgaiYZm6mbIzCkMJZZihNbMhooFtYQghE4ExpLukogRwwA4JC6ShogRC\nHBowVuqCJU7/2KuwFnJW3h/3Pfvez2fmzt597/vec66efa/u955zz63WWgAAAOjHxwzdAQAAAJ5M\nUAMAAOiMoAYAANAZQQ0AAKAzghoAAEBnBDUAAIDOCGoAAACdEdQAAAA6I6gBAAB05ug0G7v99tvb\n8ePHp9nkoD784Q/nlltuGbobHAC1HTf1HS+1HTf1HTf1Ha9Zq+073vGO322tfeJO+001qB0/fjwP\nPvjgNJsc1MbGRubn54fuBgdAbcdNfcdLbcdNfcdNfcdr1mpbVb9xI/uZ+ggAANAZQQ0AAKAzghoA\nAEBnBDUAAIDOCGoAAACdEdQAAAA6I6gBAAB0RlADAADojKAGAADQGUENAACgM0eH7gAMpaoGa7u1\nNljbMAZDnb/OXQCmxYgaM6u1tuvLHa96y56OB/bGuQvA2AlqAAAAnRHUAAAAOiOoAQAAdEZQAwAA\n6IxVH4FRsqonAHCYGVEDRsmqngDAYSaoAQAAdEZQAwAA6IygBgAA0BlBDQAAoDNWfQQAAPbEasv7\nz4gaAACwJ1Zb3n+CGgAAQGcENQAAgM4IagAAAJ0R1AAAADojqAEAAHRGUAMAAOiMoAYAANAZQQ0A\nAKAzghoAAEBnBDUAAIDOHB26AwAAV1XVYG231gZrG+BaRtQAgG601nZ9ueNVb9nT8QA9EdQAAAA6\nI6gBAAB0RlADAADojKAGAADQGUENAACgM4IaAABAZwQ1AACAzghqAAAAnRHUAAAAOiOoAQAAdEZQ\nAwAA6IygBgAA0Jkdg1pVfXJVrVfVL1fVu6vqaybbn1VVP1FV75n8/ISD7y4AAMD43ciI2uUkX9da\n+/Qkn5Pkq6vq05OcSfLW1toLkrx18jsAAAB7tGNQa629v7X2C5PrjyXZTPLcJF+c5Nxkt3NJXn5Q\nnQQAAJglT+szalV1PMlfSfKzSY611t4/uel3khzb154BAADMqKM3umNVfVySH0ryta21P6iqj9zW\nWmtV1Z7iuHuS3JMkx44dy8bGxp46fJhcunRpph7vrFHbcVPf8VLbcVPf8fK6atzU9k+7oaBWVTdl\nK6R9X2vtjZPNH6iq57TW3l9Vz0nyyPWOba3dl+S+JDl58mSbn5/fe68PiY2NjczS450p959X2zFT\n3/FS23FT31HzumrEnLvXdSOrPlaS1SSbrbVv23bTm5O8YnL9FUl+ZP+7BwAAMHtuZETt85J8RZJf\nqqqHJtu+McnZJD9QVUtJfiPJlx9MFwEAAGbLjkGttXYhST3FzXfub3cAAAC44cVEZtX2RVOmrbXr\nrs8CAACM3NNann8WtdZ2fbnjVW/Z0/EAAMBsEtQAAAA6I6gBAAB0RlADAADojKAGAADQGUENAACg\nM4IaAABAZwQ1AACAzvjCaw61F736gTz6+BODtH38zPmpt3nbzTfl4Xvvmnq7AABMl6DGofbo40/k\n4tm7p97uxsZG5ufnp97uEOEQAIDpM/URAACgM4IaAABAZwQ1AACAzghqAAAAnRHUAAAAOiOoAQAA\ndEZQAwAA6IygBgAA0BlBDQAAoDOCGgAAQGeODt0BgKfyolc/kEcff2KQto+fOT/1Nm+7+aY8fO9d\nU28XoGdra2tZWVnJ5uZm5ubmsry8nMXFxaG7BQdOUAO69ejjT+Ti2bun3u7Gxkbm5+en3u4Q4RCg\nZ2tra1leXs7q6mquXLmSI0eOZGlpKUmENUbP1EcAALq0srKS1dXVLCws5OjRo1lYWMjq6mpWVlaG\n7hocOEENAIAubW5u5tSpU0/adurUqWxubg7UI5geQQ0AgC7Nzc3lwoULT9p24cKFzM3NDdQjmB5B\nDQCALi0vL2dpaSnr6+u5fPly1tfXs7S0lOXl5aG7BgfOYiIAwL6yYiv75eqCIadPn/7Iqo8rKysW\nEmEmCGoAwL6yYiv7aXFxMYuLi4PVF4Zi6iMAAEBnBDUAAIDOCGoAAACdEdQAAAA6YzERAAYx1MqA\nVgWEw2VtbS0rKysfWfVxeXnZqo/MBEENgEEMsTKgVQHhcFlbW8vy8nJWV1dz5cqVHDlyJEtLS0ki\nrDF6pj4CANCllZWVrK6uZmFhIUePHs3CwkJWV1ezsrIydNfgwBlRAwCgS5ubmzl16tSTtp06dSqb\nm5sD9WjcfFl9XwQ1AAC6NDc3lwsXLmRhYeEj2y5cuJC5ubkBezVevqy+L6Y+AgDQpeXl5SwtLWV9\nfT2XL1/O+vp6lpaWsry8PHTX4MAZUQMAoEtXFww5ffr0R1Z9XFlZsZAIM0FQAwCgW4uLi1lcXBxs\nehwMxdRHAACAzghqAAAAnRHUAAAAOiOoAQDQrbW1tZw4cSJ33nlnTpw4kbW1taG7BFNhMREAALq0\ntraW5eXlrK6u5sqVKzly5EiWlpaSxMqPjJ4RNQAAurSyspLV1dUsLCzk6NGjWVhYyOrqalZWVobu\nGhy4mRhRe9GrH8ijjz8xSNtDfOP5bTfflIfvvWvq7Q7h1rkzeeG5M8M0fm76Td46lyR3T79hABjA\n5uZmTp069aRtp06dyubm5kA9gumZiaD26ONP5OLZ6b+4Her7PoYIh0N5bPOs2gLASM3NzeXChQtZ\nWFj4yLYLFy5kbm5uwF7BdJj6CABAl5aXl7O0tJT19fVcvnw56+vrWVpayvLy8tBdgwO344haVb0u\nyd9J8khr7cRk279N8k+SfHCy2ze21n70oDoJAMDsubpgyOnTp7O5uZm5ubmsrKxYSISZcCNTH1+f\n5DuTfO8121/bWvvWfe8RAABMLC4uZnFxcbCPHcBQdpz62Fp7W5IPTaEvAAAAZG+Libyyqr4yyYNJ\nvq619nvX26mq7klyT5IcO3YsGxsbe2hy94Zo99KlSzP1eIeituOmvuM27certtPj3GW/DVnfWeLc\n7cdug9p3Jfl3Sdrk579P8o+vt2Nr7b4k9yXJyZMn2yBD1vefH2SofLAh+oEe7yDUdtzUd9wGeLxq\nOyXOXQ6AqY9T4Nztyq5WfWytfaC1dqW19sdJvjvJZ+9vtwAAAGbXroJaVT1n269fkuRd+9MdAAAA\nbmR5/rUk80lur6r3Jbk3yXxVvThbUx8vJvmnB9hHAACAmbJjUGutXe+LKlYPoC8AAABkb6s+AgD8\nKbfOnckLz50ZpvFz02/y1rkkuXv6DQOjJqgBAPvqsc2zuXh2+sFlqJXjjp85P/U2gfHb1WIiAAAA\nHBxBDQAAoDOCGgAAQGcENQAAgM4IagAAAJ0R1AAAADojqAEAAHRGUAMAAOiMoAYAANAZQQ0AAKAz\nR4fuwDTcOncmLzx3ZpjGz02/yVvnkuTu6TcM+8y5CwDMqpkIao9tns3Fs9N/8bOxsZH5+fmpt3v8\nzPmptwkHwbkLAMwqUx8BAAA6I6gBAAB0RlADAADojKAGAADQGUENAACgM4IaAABAZwQ1AACAzghq\nAAAAnRHUAAAAOiOoAQAAdObo0B0AAGA2VNVgbbfWBmsbdsOIGgAAU9Fa2/Xljle9ZU/Hw2EjqAEA\nAHRGUAMAAOiMoAYAANAZQQ0AAKAzVn3k0Dt+5vwwDd8//XZvu/mmqbcJAMD0CWocahfP3j1Iu8fP\nnB+sbQAAxs/URwAAgM4IagAAAJ0R1AAAADojqAEAAHRmZhYTsTIgAABwWMxEULMyIAAAcJiY+ggA\nANAZQQ0AAKAzghoAAEBnBDUAAIDOCGoAAACdEdQAAAA6MxPL8wMA0+X7SwH2RlADAPaV7y8F2DtT\nHwEAADpjRA0AgBv2olc
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa781a83f98>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[[\"Techno\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"# DNB pro\n",
"\n",
"On ne parle plus que des DNB pro maintenant"
]
},
{
"cell_type": "code",
"execution_count": 49,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"['305', '306', '307', '308', '312']"
]
},
"execution_count": 49,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"pro"
]
},
{
"cell_type": "code",
"execution_count": 28,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"sheets_pro = pd.read_excel(\"./DNB blanc 1.xls\",\n",
" sheetname=pro,\n",
" skiprows=[0],\n",
" parse_cols=\"B,C,E,G,I,K,M\",\n",
" )\n",
"\n",
"df = orderedDict2df(sheets_pro)"
]
},
{
"cell_type": "code",
"execution_count": 29,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"#df.head()"
]
},
{
"cell_type": "code",
"execution_count": 30,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df.columns = [\"Nom\", \"Français\", \"HG\", \"Maths\", \"SVT\", \"Physique\", \"Techno\", \"Classe\"]"
]
},
{
"cell_type": "code",
"execution_count": 31,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"for m, coef in coeff.items():\n",
" df[m] = pd.to_numeric(df[m], errors='coerce')\n",
" df[\"_\"+m] = df[m]/coef\n",
"#df.head()"
]
},
{
"cell_type": "code",
"execution_count": 32,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df = df = df.assign(\n",
" total = df[matieres].sum(1),\n",
" maximum = 325\n",
")\n",
"df = df.assign(\n",
" normalisee = df[\"total\"]/df[\"maximum\"]\n",
")"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"Elèves absent à au moins une epreuve"
]
},
{
"cell_type": "code",
"execution_count": 33,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
2018-04-10 11:22:39 +00:00
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Nom</th>\n",
2018-04-12 18:06:58 +00:00
" <th>Classe</th>\n",
2018-04-10 11:22:39 +00:00
" <th>Français</th>\n",
" <th>HG</th>\n",
" <th>Maths</th>\n",
" <th>SVT</th>\n",
" <th>Physique</th>\n",
" <th>Techno</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>5</th>\n",
" <td>ALI CHIONI Azihar</td>\n",
" <td>305</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>19</th>\n",
" <td>YOUSSOUF Radika</td>\n",
" <td>305</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>10</th>\n",
" <td>IBRAHIM Izaki (UPE2A)</td>\n",
" <td>306</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>12.0</td>\n",
" <td>5.5</td>\n",
" <td>NaN</td>\n",
" <td>2.0</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>ALI MROIVILI Rasmine</td>\n",
" <td>307</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>5</th>\n",
" <td>AN-YALDINE Mourtaza</td>\n",
" <td>307</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
2018-04-10 11:22:39 +00:00
" <th>0</th>\n",
2018-04-12 18:06:58 +00:00
" <td>ABDOU Mounibati</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
2018-04-12 18:06:58 +00:00
" <td>AHAMED Halima</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>6</th>\n",
" <td>ANDILI Hafidhou</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>21</th>\n",
" <td>MOUSTOIFA Edé</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>22</th>\n",
" <td>MROIVILI Abdou</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>23</th>\n",
" <td>MZE El Anziz</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" <tr>\n",
" <th>24</th>\n",
" <td>RABEHAMINA Jessica</td>\n",
" <td>308</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" <td>NaN</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" Nom Classe Français HG Maths SVT Physique Techno\n",
"5 ALI CHIONI Azihar 305 NaN NaN NaN NaN NaN NaN\n",
"19 YOUSSOUF Radika 305 NaN NaN NaN NaN NaN NaN\n",
"10 IBRAHIM Izaki (UPE2A) 306 NaN NaN 12.0 5.5 NaN 2.0\n",
"3 ALI MROIVILI Rasmine 307 NaN NaN NaN NaN NaN NaN\n",
"5 AN-YALDINE Mourtaza 307 NaN NaN NaN NaN NaN NaN\n",
"0 ABDOU Mounibati 308 NaN NaN NaN NaN NaN NaN\n",
"1 AHAMED Halima 308 NaN NaN NaN NaN NaN NaN\n",
"6 ANDILI Hafidhou 308 NaN NaN NaN NaN NaN NaN\n",
"21 MOUSTOIFA Edé 308 NaN NaN NaN NaN NaN NaN\n",
"22 MROIVILI Abdou 308 NaN NaN NaN NaN NaN NaN\n",
"23 MZE El Anziz 308 NaN NaN NaN NaN NaN NaN\n",
"24 RABEHAMINA Jessica 308 NaN NaN NaN NaN NaN NaN"
]
},
"execution_count": 33,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"absents = df[df.isnull().any(1)]\n",
"absents[[\"Nom\", \"Classe\"]+matieres]"
]
},
{
"cell_type": "code",
"execution_count": 34,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"df = df[~df.isnull().any(1)]"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Répartition des notes"
]
},
{
"cell_type": "code",
"execution_count": 35,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78189b5f8>"
]
},
"execution_count": 35,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA20AAAEyCAYAAABptTjBAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGdpJREFUeJzt3X+spXldH/D3x52Vmh1drEtGOqwdWlcTw6YKN0BjNXe0\n6gKG7Q9slxgEqxk1YDXFlMUmaEmarrZoVIyUBgIYZKAgcQPbKlVG9A+Ume2WYXclDnYNs253C2sH\nr6zakU//uGeXy51z7z137jn3fGfu65XczDnP+Z7n+Tznc77POe85zz23ujsAAACM6YuWXQAAAABb\nE9oAAAAGJrQBAAAMTGgDAAAYmNAGAAAwMKENAABgYEIbAADAwIQ2AACAgQltAAAAAzu0rA3fcMMN\nfezYsWVtfl/8+Z//ea677rpll8E29Ghs+jM+PRqb/oxPj8amP+O70nt05syZT3X3U3Yat7TQduzY\nsZw+fXpZm98Xp06dyurq6rLLYBt6NDb9GZ8ejU1/xqdHY9Of8V3pPaqqP55lnNMjAQAABia0AQAA\nDExoAwAAGJjQBgAAMDChDQAAYGBCGwAAwMCENgAAgIEJbQAAAAPbMbRV1d+oqt+vqv9ZVfdW1b+d\nMuZJVfXOqjpXVb9XVccWUSwAAMBBM8snbX+Z5Fu6++8l+fokt1TVczeN+b4kf9rdX53kZ5P81HzL\nBAAAOJh2DG29bm1y9drJT28admuSt04uvzvJt1ZVza1KAACAA6q6N+evKYOqrklyJslXJ/nF7n7V\npts/luSW7j4/uf6JJM/p7k9tGnciyYkkOXLkyLNOnjw5l50Y1draWg4fPjz39Z598MIly24+ev3c\ntzPKdhdpY4+uxv3baNr+TTPSPi9qDjE/enR59ut4M2t/rvbj38jMobHpz/iu9B4dP378THev7DRu\nptD2xOCqJyd5b5If7u6PbVg+U2jbaGVlpU+fPj3ztq9Ep06dyurq6tzXe+z291+y7IE7XjD37Yyy\n3UXa2KOrcf82mrZ/04y0z4uaQ8yPHl2e/TrezNqfq/34NzJzaGz6M74rvUdVNVNo29W3R3b3/03y\nwSS3bLrpwSQ3TjZ8KMn1ST69m3UDAABwqVm+PfIpk0/YUlVfkuTbkvzBpmF3Jnnp5PKLkvxW7+Yj\nPAAAAKY6NMOYpyZ56+T32r4oybu6+31V9dokp7v7ziRvSvLLVXUuyaNJbltYxQAAAAfIjqGtuz+a\n5BumLH/Nhst/keS75lsaAAAAu/qdNgAAAPaX0AYAADAwoQ0AAGBgQhsAAMDAhDYAAICBCW0AAAAD\nE9oAAAAGJrQBAAAMTGgDAAAYmNAGAAAwMKENAABgYEIbAADAwIQ2AACAgQltAAAAAxPaAAAABia0\nAQAADExoAwAAGJjQBgAAMDChDQAAYGBCGwAAwMCENgAAgIEJbQAAAAMT2gAAAAYmtAEAAAxMaAMA\nABiY0AYAADAwoQ0AAGBgQhsAAMDAhDYAAICBCW0AAAADE9oAAAAGJrQBAAAMTGgDAAAYmNAGAAAw\nsB1DW1XdWFUfrKr7qureqvqRKWNWq+pCVd0z+XnNYsoFAAA4WA7NMOZikld2991V9aVJzlTVB7r7\nvk3jfqe7v3P+JQIAABxcO37S1t0Pdffdk8t/luT+JEcXXRgAAABJdffsg6uOJflQkmd092c2LF9N\n8p4k55P8SZIf6+57p9z/RJITSXLkyJFnnTx5cg+lj29tbS2HDx+e+3rPPnjhkmU3H71+7tsZZbuL\ntLFHV+P+bTRt/6YZaZ8XNYeYHz26PPt1vJm1P1f78W9k5tDY9Gd8V3qPjh8/fqa7V3YaN3Noq6rD\nSX47yb/r7l/ddNuXJflcd69V1fOT/Fx337Td+lZWVvr06dMzbftKderUqayurs59vcduf/8lyx64\n4wVz384o212kjT26Gvdvo2n7N81I+7yoOcT86NHl2a/jzaz9udqPfyMzh8amP+O70ntUVTOFtpm+\nPbKqrs36J2lv3xzYkqS7P9Pda5PLdyW5tqpu2GXNAAAAbDLLt0dWkjclub+7f2aLMV85GZeqevZk\nvZ+eZ6EAAAAH0SzfHvmNSV6S5GxV3TNZ9uNJvipJuvsNSV6U5Ieq6mKSx5Lc1rv5ZTkAAACm2jG0\ndffvJqkdxrw+yevnVRQAAADrZvqdNgAAAJZDaAMAABiY0AYAADAwoQ0AAGBgQhsAAMDAhDYAAICB\nCW0AAAADE9oAAAAGJrQBAAAMTGgDAAAYmNAGAAAwMKENAABgYEIbAADAwIQ2AACAgQltAAAAAxPa\nAAAABia0AQAADExoAwAAGJjQBgAAMDChDQAAYGBCGwAAwMCENgAAgIEJbQAAAAMT2gAAAAYmtAEA\nAAxMaAMAABiY0AYAADAwoQ0AAGBgQhsAAMDAhDYAAICBCW0AAAADE9oAAAAGJrQBAAAMTGgDAAAY\n2I6hrapurKoPVtV9VXVvVf3IlDFVVT9fVeeq6qNV9czFlAsAAHCwHJphzMUkr+zuu6vqS5OcqaoP\ndPd9G8Y8L8lNk5/nJPmlyb8AAADswY6ftHX3Q9199+TynyW5P8nRTcNuTfK2XvfhJE+uqqfOvVoA\nAIADprp79sFVx5J8KMkzuvszG5a/L8kd3f27k+u/meRV3X160/1PJDmRJEeOHHnWyZMn91r/0NbW\n1nL48OGpt5198MIly24+ev1M46aZdt95m7WWafajvq1s91hv7NGsPdkve6lnP3q1H4/XdnNonvXs\nZT4u8zkygkUd50Z7XOd9LN6vfZ51Dl0JPbha7eY4N80iXiv0/vP22h8W70rv0fHjx89098pO42Y5\nPTJJUlWHk7wnyY9uDGy70d1vTPLGJFlZWenV1dXLWc0V49SpU9lqH192+/svWfbAd186dtq4aabd\nd95mrWWa/ahvK9s91ht7NGtP9ste6tmPXu3H47XdHJpnPXuZj8t8joxgUce50R7XeR+L92ufZ51D\nV0IPrla7Oc5Ns4jXCr3/vL32h8U7KD2a6dsjq+rarAe2t3f3r04Z8mCSGzdcf9pkGQAAAHswy7dH\nVpI3Jbm/u39mi2F3JvmeybdIPjfJhe5+aI51AgAAHEiznB75jUlekuRsVd0zWfbjSb4qSbr7DUnu\nSvL8JOeSfDbJ986/VAAAgINnx9A2+XKR2mFMJ3n5vIoCAABg3Uy/0wYAAMByCG0AAAADE9oAAAAG\nJrQBAAAMTGgDAAAYmNAGAAAwMKENAABgYEIbAADAwIQ2AACAgQltAAAAAxPaAAAABia0AQAADExo\nAwAAGJjQBgAAMDChDQAAYGBCGwAAwMCENgAAgIEJbQAAAAMT2gAAAAYmtAEAAAxMaAMAABiY0AYA\nADAwoQ0AAGBgQhsAAMDAhDYAAICBCW0AAAADE9oAAAAGJrQBAAAMTGgDAAAYmNAGAAAwMKENAABg\nYEIbAADAwIQ2AACAgQltAAAAA9sxtFXVm6vqkar62Ba3r1bVhaq6Z/LzmvmXCQAAcDAdmmHMW5K8\nPsnbthnzO939nXOpCAAAgCfs+Elbd38oyaP7UAsAAACbVHfvPKjqWJL3dfczpty2muQ9Sc4n+ZMk\nP9bd926xnhNJTiTJkSNHnnXy5MnLrfuKsLa2lsOHD0+97eyDFy5ZdvPR62caN820+87brLVMsx/1\nbWW7x3pjj2btyX7ZSz370av9eLy2m0PzrGcv83GZz5ERLOo4N9rjOu9j8X7t86xz6ErowdVqN8e5\naRbxWqH3n7fX/rB4V3qPjh8/fqa7V3YaN4/Q9mVJPtfda1X1/CQ/19037bTOlZWVPn369I7bvpKd\nOnUqq6urU287dvv7L1n2wB0vmGncNNPuO2+z1jLNftS3le0e6409mrUn+2Uv9exHr/bj8dpuDs2z\nnr3Mx2U+R0awqOPcaI/rvI/F+7XPs86hK6EHV6vdHOemWcRrhd5/3l77w+Jd6T2qqplC256/PbK7\nP9Pda5PLdyW5tqpu2Ot
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa78189bac8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[\"total\"].hist(bins=150, figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Statistiques par matières et le total"
]
},
{
"cell_type": "code",
"execution_count": 36,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>Français</th>\n",
" <th>HG</th>\n",
" <th>Maths</th>\n",
" <th>SVT</th>\n",
" <th>Physique</th>\n",
" <th>Techno</th>\n",
" <th>total</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" <td>100.00</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td>25.92</td>\n",
" <td>15.76</td>\n",
" <td>24.30</td>\n",
" <td>9.18</td>\n",
" <td>6.28</td>\n",
" <td>7.14</td>\n",
" <td>88.58</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td>18.62</td>\n",
" <td>7.57</td>\n",
" <td>14.35</td>\n",
" <td>5.02</td>\n",
" <td>3.98</td>\n",
" <td>3.87</td>\n",
" <td>45.41</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
2018-04-10 11:22:39 +00:00
" <td>1.00</td>\n",
2018-04-12 18:06:58 +00:00
" <td>2.00</td>\n",
" <td>5.00</td>\n",
" <td>2.50</td>\n",
" <td>2.00</td>\n",
" <td>2.00</td>\n",
" <td>20.50</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>25%</th>\n",
" <td>9.50</td>\n",
" <td>9.00</td>\n",
" <td>14.38</td>\n",
" <td>4.50</td>\n",
" <td>3.00</td>\n",
" <td>4.00</td>\n",
" <td>51.88</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td>21.50</td>\n",
" <td>15.00</td>\n",
" <td>21.00</td>\n",
" <td>9.00</td>\n",
" <td>5.00</td>\n",
" <td>6.75</td>\n",
" <td>78.75</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>41.50</td>\n",
" <td>21.00</td>\n",
" <td>29.62</td>\n",
" <td>13.00</td>\n",
" <td>8.25</td>\n",
" <td>9.00</td>\n",
" <td>122.38</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" <tr>\n",
2018-04-12 18:06:58 +00:00
" <th>max</th>\n",
" <td>68.00</td>\n",
" <td>34.00</td>\n",
" <td>81.00</td>\n",
" <td>20.00</td>\n",
" <td>21.00</td>\n",
" <td>20.50</td>\n",
" <td>202.50</td>\n",
2018-04-10 11:22:39 +00:00
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
2018-04-12 18:06:58 +00:00
" Français HG Maths SVT Physique Techno total\n",
"count 100.00 100.00 100.00 100.00 100.00 100.00 100.00\n",
"mean 25.92 15.76 24.30 9.18 6.28 7.14 88.58\n",
"std 18.62 7.57 14.35 5.02 3.98 3.87 45.41\n",
"min 1.00 2.00 5.00 2.50 2.00 2.00 20.50\n",
"25% 9.50 9.00 14.38 4.50 3.00 4.00 51.88\n",
"50% 21.50 15.00 21.00 9.00 5.00 6.75 78.75\n",
"75% 41.50 21.00 29.62 13.00 8.25 9.00 122.38\n",
"max 68.00 34.00 81.00 20.00 21.00 20.50 202.50"
]
},
"execution_count": 36,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"round(df[matieres+[\"total\"]].describe(), 2)"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Données par matières\n",
"\n",
"On a rapporté les notes sur 1 pour pouvoir comparer les matières entre elles."
]
},
{
"cell_type": "code",
"execution_count": 37,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78189bb00>"
]
},
"execution_count": 37,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA20AAAEzCAYAAACi6etkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAH+dJREFUeJzt3X+UpXddH/D3x13YpJDGlnhShMBSiXaWjUFcg+K2zDRI\noSjo0QpToKJr0rVlW130ZGUsCLia9QetRnSbsNgcwQn+ao1s+FHjjLqiloACIaM2RX4k1AIqOSwm\nSzZ++8d9NsxuJtk7u3dyn7nzep2z59z73O995jN3vnvv877f7/N9qrUWAAAA+umLxl0AAAAAD05o\nAwAA6DGhDQAAoMeENgAAgB4T2gAAAHpMaAMAAOgxoQ0AAKDHhDYAAIAeE9oAAAB6bPO4fvAFF1zQ\ntm7dOq4f31uf+9zn8qhHPWrcZbAO6Cushv7CsPQVVkN/YVj6ysre+973frq19iWnaze20LZ169bc\ncsst4/rxvbW4uJjp6elxl8E6oK+wGvoLw9JXWA39hWHpKyurqo8O0870SAAAgB4T2gAAAHpMaAMA\nAOgxoQ0AAKDHhDYAAIAeE9oAAAB6TGgDAADoMaENAIBVmZ+fz/bt23P55Zdn+/btmZ+fH3dJMNHG\ndnFtAADWn/n5+czNzeXQoUO57777smnTpuzatStJMjs7O+bqYDIZaQMAYGj79+/PoUOHMjMzk82b\nN2dmZiaHDh3K/v37x10aTCyhDQCAoS0tLWXnzp0nbdu5c2eWlpbGVBFMPqENAIChTU1N5ciRIydt\nO3LkSKampsZUEUw+oQ0AgKHNzc1l165dWVhYyPHjx7OwsJBdu3Zlbm5u3KXBxLIQCQAAQzux2Mie\nPXuytLSUqamp7N+/3yIkrGh+fj779++/v6/Mzc3pK2dAaAMAYFVmZ2czOzubxcXFTE9Pj7scespK\no6NjeiQAADByVhodHaENYIK5AC4A42Kl0dExPRJgQpmWAsA4nVhpdGZm5v5tVho9M0baACaUaSkA\njJOVRkdnqJG2qnpOkp9OsinJG1trV5/y+BOSXJ/ki7s2+1prN424VgBWwbQUAMbJSqOjc9qRtqra\nlOQNSZ6bZFuS2aradkqzH0ryy621r0ryoiQ/N+pCAVgdF8AFYNxmZ2dz66235uabb86tt94qsJ2h\nYaZHXpbk9tbah1trn09yQ5IXnNKmJfn73e3zk3xidCUCcCZMSwGAyVCttYduUPVtSZ7TWvvu7v5L\nkzy9tfbyZW0em+RdSf5BkkcleVZr7b0r7OvKJFcmyYUXXvjVN9xww6h+j4lx9OjRPPrRjx53GawD\n+grDuPnmm/PmN785H/vYx/KEJzwhL3nJS3L55ZePuyzWyPKT/ftgYWFh3CWwxnwWMSx9ZWUzMzPv\nba3tOF27UYW2vd2+fqqqvi7JoSTbW2t/92D73bFjR7vllluG+202EBepZFj6CquhvzCsrfsO5yNX\nP2/cZbBOeG9hWPrKyqpqqNA2zPTIO5NctOz+47tty+1K8stJ0lr7gyTnJLlguFIBAAB4MMOEtvck\nubiqnlRVj8xgoZEbT2nzsSSXJ0lVTWUQ2j41ykIBAAA2otOGttba8SQvT/LOJEsZrBL5oap6bVU9\nv2v2iiRXVNX7k8wneVk73bxLAAAATmuo67R111y76ZRtr1p2+7YkXz/a0gAAABhmeiQAAABjIrQB\nAAD0mNAGAADQY0IbAABAjwltAAAAPSa0AQAA9JjQBgAA0GNCGwAAQI8JbQAAAD0mtAEAAGtiz549\nOeecczIzM5Nzzjkne/bsGXdJ69LmcRcAAABMnj179uTgwYM5cOBAtm3blttuuy1XXXVVkuSaa64Z\nc3Xri5E2AABg5K677rocOHAge/fuzTnnnJO9e/fmwIEDue6668Zd2rojtAEAACN37Nix7N69+6Rt\nu3fvzrFjx8ZU0foltAEAACO3ZcuWHDx48KRtBw8ezJYtW8ZU0frlnDYAAGDkrrjiivvPYdu2bVte\n//rX56qrrnrA6BunJ7QBAAAjd2KxkVe+8pU5duxYtmzZkt27d1uE5AyYHgkAAKyJa665Jvfcc08W\nFhZyzz33CGxnSGgDAADoMaENAACgx4Q2AACAHhPaAAAAekxoA5hg8/Pz2b59ey6//PJs37498/Pz\n4y4JgA3E59BoWPIfYELNz89nbm4uhw4dyn333ZdNmzZl165dSZLZ2dkxVwfApPM5NDpG2gAm1P79\n+3Po0KHMzMxk8+bNmZmZyaFDh7J///5xlwbABuBzaHSENoAJtbS0lJ07d560befOnVlaWhpTRQBs\nJD6HRkdoA5hQU1NTOXLkyEnbjhw5kqmpqTFVBMBG4nNodIQ2gAk1NzeXXbt2ZWFhIcePH8/CwkJ2\n7dqVubm5cZcGwAbgc2h0LEQCMKFOnOS9Z8+eLC0tZWpqKvv373fyN3DW9uzZk+uuuy7Hjh3Lli1b\ncsUVV+Saa64Zd1n0jM+h0RHaACbY7OxsZmdns7i4mOnp6XGXA0yAPXv25ODBgzlw4EC2bduW2267\nLVdddVWSCG48gM+h0TA9EgCAoV133XU5cOBA9u7dm3POOSd79+7NgQMHct111427NJhYRtpGpKrG\nXcJJWmvjLoGHoL8AsF4dO3Ysu3fvPmnb7t2784pXvGJMFcHkM9I2Iq21kfx74lVvG8l+6Lc+9RX9\nBYDV2LJlSw4ePHjStoMHD2bLli1jqggmn5E2AACGdsUVV9x/Dtu2bdvy+te/PlddddUDRt+A0RHa\nAAAY2onFRl75ylfev3rk7t27LUICa8j0SAAAVuWaa67JPffck4WFhdxzzz0CG6wxoQ0AAKDHhDYA\nAIAeE9oAAAB6TGgDAADoMaENAACgx4Q2AACAHhPaAAAAekxoAwAA6DGhDQAAoMeENgAAgB4T2gAA\nAHpMaAMAAOgxoQ0AAKDHhDaACTY/P5/t27fn8ssvz/bt2zM/Pz/ukgCAVdo87gIAWBvz8/OZm5vL\noUOHct9992XTpk3ZtWtXkmR2dnbM1QEAwzLSBjCh9u/fn0OHDmVmZiabN2/OzMxMDh06lP3794+7\nNABgFYYKbVX1nKr6s6q6var2PUibb6+q26rqQ1X1S6MtE4DVWlpays6dO0/atnPnziwtLY2pIgDg\nTJw2tFXVpiRvSPLcJNuSzFbVtlPaXJzkB5N8fWvtKUm+dw1qBWAVpqamcuTIkZO2HTlyJFNTU2Oq\nCAA4E8OMtF2W5PbW2odba59PckOSF5zS5ookb2it/U2StNY+OdoyAVitubm57Nq1KwsLCzl+/HgW\nFhaya9euzM3Njbs0AGAVhlmI5HFJPr7s/h1Jnn5Kmy9Pkqr6/SSbkvxwa+0dp+6oqq5McmWSXHjh\nhVlcXDyDkief14Vh6Ss8lMc+9rF58YtfnO/6ru/Kxz72sTzhCU/IS17ykjz2sY/Vd3hI+sfkm5mZ\nGXcJJ1lYWBh3Cayxo0ePem85C6NaPXJzkouTTCd5fJLfrapLWmufWd6otXZtkmuTZMeOHW16enpE\nP36CvONwvC4MRV9hCNPT03nd616XxcVF/YXheG/ZEFprI9nP1n2H85GrnzeSfTHZfA6dnWGmR96Z\n5KJl9x/fbVvujiQ3ttbuba39RZI/zyDEAQAAcBaGCW3vSXJxVT2pqh6Z5EVJbjylzf/IYJQtVXVB\nBtMlPzzCOgE4Ay6uDQDr32mnR7bWjlfVy5O8M4Pz1d7UWvtQVb02yS2ttRu7x55dVbcluS/JD7TW\n/motCwfgobm4NgBMhqGu09Zau6m19uWttS9rre3vtr2qC2xpA3tba9taa5e01m5Yy6IBOD0X1waA\nyTBUaANg/XFxbQCYDEIbwIRycW0AmAxCG8CEcnFtAJgMo7pOGwA9Mzs7m3e/+9157nOfm2PHjmXL\nli254oorLEICAOuM0AYwoebn53P48OG8/e1vP2n1yGc84xmCGwCsI6ZHAkwoq0cCwGQw0gYwoawe\nCcAoVNW4SzhJa23cJTz
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa7818eaa58>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"df[norm_matieres].boxplot(figsize=(15,5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"### Y a-t-il un lien entre la réussite dans une matière et dans une autre?"
]
},
{
"cell_type": "code",
"execution_count": 38,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"from pandas.plotting import scatter_matrix"
]
},
{
"cell_type": "code",
"execution_count": 39,
"metadata": {
"scrolled": false,
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3YAAANgCAYAAABgIvoLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd449d54PvvQW8E2Huf3qukkUZWsSSrxHKRbLlJjp1i\n+8a58XWye3Nzn93c3exuNrvOxvETPyneZLOxY8VVtmVZtqLiImmk6b2zd4IASPSOc/8ASU0hhyCJ\nzvN5Hj3iDAjgDPArp7znfYWUEkVRFEVRFEVRFKV0aQrdAEVRFEVRFEVRFGV11MBOURRFURRFURSl\nxKmBnaIoiqIoiqIoSolTAztFURRFURRFUZQSpwZ2iqIoiqIoiqIoJU4N7BRFURRFURRFUUqcGtgp\niqIoiqIoiqKUODWwUxRFURRFURRFKXFqYKcoiqIoiqIoilLidIVuwGJqa2tlZ2dnoZuhlIiBgQHU\n8aJkQh0rynKo40XJlDpWlOVQx4uSqePHj7uklHWZ/G7RDuw6Ozs5duxYoZuhlIj9+/er40XJiDpW\nlOVQx4uSKXWsKMuhjhclU0KIwUx/t2gHdoqi5I83FOe5kyMkU5IP7mmhxmYsdJPKzomhad7qdbOu\nzsrD2xoRQhS6SYpSFF67NMnFcT9726u4c11NoZtTctS1RSkXUkp+em6CfleQg+tr2d1WWegmlRy1\nx05RFHpdAWZCcfyRBFcmA4VuTlk6MzxDLJHi4rifcDxZ6OYoSlFIpSSnh73EEilOj8wUujklSV1b\nlHIRiiW5POEnlkhxRl0PVkQN7BRFobvWSoVJh82oY329rdDNKUs7Wh1oNYKNDRWY9dpCN0dRioJG\nI9jRkj43drY4Ct2ckqSuLUq5sBi0rK+3odUItqvrwYqsmVBMbyjO+TEvNpOObc3pi6CiKGmVFgO/\n9a7uQjejrO3rqGZfR3Whm6EoRefBrQ08uLWh0M0oWeraopQLIQSP72oudDNKWtkP7JIpyV//vIev\n/ryHaCIFQGeNhT97cicHulUsv6IoiqIoiqIopa+sQzGllPzh98/wP16+woNbG/jn37yDL39kF0II\nPv4/3+bHp8cK3URFURRFURRFUZRVK+sVu394o5/vHR/h9x7YwBcf3DCfKeqhrY38xj8e5YvfPkWT\nw8T+ThXCoCiKoiiKoihK6SrbFbsep5///tJlHtracN2gDsBm1PH3n9pPS5WZ3332JN5QvIAtVRRF\nURRFURRFWZ2yHdj91xcvYdRp+NMP7liwpovdpOerH9uL0x/hv790qQAtVBRFURRFURRFyY6yHNgd\nG/Dw6iUnn7t3HXUVixda3tHq4FN3dfHskSFVL0NRFEVRFEVRlJJVlgO7v3qth1qbkU8f7Fzyd7/4\n0AaqLAa+9NLl3DdMUQokmZL0OP1MB2OFboqyhkgp6Z0K4ApEC90UZQUGXEEmfZFCN0NRsi4ST3J1\n0k8olih0U9aEaCL9efsjautTrpXdwK5vKsAvr0zxzIEOLIalc8NUmPT8H/eu4/WrLg73ufPQQkXJ\nv19cdvLj0+M8e2SIYLR4b2ROf4RLEz6SKVnoppSdYU+I3qlAXt/zUK+b50+N8ezhITWpUGJODE3z\ng5Oj/MuRISa8pTO480XiXBjzEYknC90UpYh9++gQ//jmAF9/a7DQTSkb3vDi596LZ8d54cw43zoy\nrO7vOVZ2A7uvvzWIXiv42B1tGT/nmTs7qK8w8uVXruSwZYpSOIHZwVwskZqv51hsvOE43z4yzE/P\nTvCrK1OFbk5ZGfaE+N7xEZ4/Ncap4fyFnc8dd8mUJKw62iVlbgJISgiWyKqGlJLvHB3mpfMTPH9K\nlTNSFvd2n4feqQCH+9xIqQYaq5VKSb59dIiXzk8sWEosEElfQ8LxpBrY5VhZlTuIxJN8//gIj+1o\nor7ClPHzTHotn7mnm//8k4ucHfGyo9WRw1YqSv7dt6meCpOHBruJaquh0M1ZUDyZIjF7wVeDgOy6\n9vMMx/L32d69vhaDVkO11UBzpTlv76us3m2d1aQkWA1aumuthW5ORlKS+dUCdQ1RbmVDvY1+V5Cm\nysz7isriUlISjacnjRdasXt4eyNnhr1011kx6MpuTamo5HRgJ4T4JPDrgBb4BPBvgP3ACSnlF7L9\nfj+/5MQfTfDhfZmv1s156rY2/vKVq/zDG3385Uf3ZLtpipJTTn+EQXeITY0V2E36mx53mPW8e3ND\nAVqWuVqbkUe2NzLlj7Kvo6rQzSkrG+pt3LOxjmgiyf7OzD7b0Zkw4zNhtjU7MBu0K3pfq1HH/Zvr\nV/RcpbBMei33bqxb9HF3IEqfK8iGehuVluKYLNJqBO/f3ULPVIDtzWqCFsAfiXNpwk97tYUGuxrE\nzPnEgQ4ujPvY2FCxYOZ0ZXl0Wg3v391CryvAjpabz736ChMPbs3+8dfj9OOPJNjR4kCnVQNGyOHA\nTgjRAtwrpXxg9s97AZuU8l1CiL8RQtwmpTyazff80akxam1G7lxXs+zn2k16ntrfxtffGuAPH91M\nk0PNLiulIZmSfO/4CNF4iiuTfj5xR0ehm7RiW5rsbGnK/PdDsQRnRrw0OUx01JTGqkI2eUNxLoz7\n6Ky13PKaJYRY1mA5GE3w3PEREinJ6EyY9+9uyUZzlTLy/RMjBKNJzo96+dTBrkI3Z15btYW2aktG\nvxtLpDg9MoPDrGdjQ0WOW1YYL54dZ2wmgkGn4TP3dKMvYOd3JhTj4rifrlorjY7CDjIb7CY10M2y\n9hoL7TWZnXu3MjIdYtgTZluLfcGJ6mt/78enxwEIxZIcXF+76vcuB7k8wx8GtEKIV4UQfwXcCbw8\n+9grs3/OGm84zmuXnDy+qwmtZmWzL58+2ElKSr6hNtMqSkl4+cIkb/W6+eHJsTWZbeuFs2O83efm\nuROjxJPZ2zupJrCVteDNHhdvXHXxkzPjjHvDhW5O2fvxmXHe7nPz/RMjap+VsqBIPMkPTozydp+b\nn52duOXvqpXWheUyFLMBMEgpHxBC/DfAAfTOPuYFtt34BCHEZ4DPALS3ty/rzf71/ASxZGpVM8tt\n1Rbevbme7x4f4YsPbSzozJaiZEqrEXxoX+t8KOZKpFKS40PTJFOS/R1VJRPSoNOk26kRoCnzi3zv\nVIBhT4jdbZXzoW+62UksjRBk819vMeh4Yl/rfCimotzoyb2t86GYpWpuElgI0AqBJxjjzMgMnTVW\nOktkX+FSHtvRxOUJP23VlmX1aVyBKGdHvXTXWrMWDaGdvUZrNdm9Xim5Mx2McXpkhvZqC911uT/X\nNUKg0QhIySUXaVoqzTy+qxl/JL5g+OdalcuBnRf45ezPr5HeW2ef/bMduCk1m5Tya8DXAPbv37+s\n6ZxXLk7S7DCxa5WJTz56WzuvXDzGqxedPLK9cVWvpSj5Ul9hWlbCoBtdGPfxxlUXAHqtpmT2uD24\ntZ6WKjMNdiNWY1nlgrpOKJbghdPjpKTE6Yvy1G3pfcTv3dnMlcl0py3bg/GWSjMtKuGJsogam5Ea\nm7HQzViVu9bVUGUx4DDrqbebePbwEJO+CGdGvHz23m6MupXtLS0mFSY9+zurl/28n56bwOWPcm7E\ny+fuW5eVie737W7m6mR6v59mhZFVSn7964UJxmYinB728pl7ule83zpTBp2GD+9vZXQ6zOZG+5K/\nv76EJ5ZyJZfT8oeAnbM/7wYk8MDsnx8E3s7WG0XiSV6/6uLdW+pXvTR736Y6GuxGvnV0KEutU5Ti\nd+3F2qwvnc6MUadld1tl2e+J1WrEfCaxa78rq1HHnvYqaku8g60ohaDTatjR6pjfF2Q2pM8xo04z\nv7q0Vs3dB4x6TdaiIWyz16tSnxBYS0yzx4FBp1nxNqflqq8wsae9KueDyHKVsyluKeUpIURYCPEL\nwAV8HPiSEOJ14JSU8ki23uvtPjehWJIHspD1T6fV8NT+Nr768x5GZ8JqxlpZE9bV2XhybytJKekq\nkxCkcmLUafnobW1M+CK
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa7818f0198>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"ax = scatter_matrix(df[matieres],\n",
" alpha=0.5,\n",
" figsize=(15, 15),\n",
" diagonal='kde')"
]
},
{
"cell_type": "code",
"execution_count": 40,
"metadata": {
"scrolled": false,
"slideshow": {
"slide_type": "slide"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAABGsAAAQwCAYAAABSYNOpAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3XlwHOl55/nvW5VVlXWiqnAfvJsUyW51S012q9WSrcOW\nbI3b8k7YHtuzMR7vhq+1PbPhCXvGjph12JqZtXd2RmHZ64hdjWzvetfHzrHj0dpay5cky+pWd5M6\n+iApsg81CYAkjgJQZ1ZWVr77RwJgoVBAHagqoIDnE4Fgo5gAko3f+2bWm+/7vEprjRBCCCGEEEII\nIYQ4GHz7fQJCCCGEEEIIIYQQ4gEZrBFCCCGEEEIIIYQ4QGSwRgghhBBCCCGEEOIAkcEaIYQQQggh\nhBBCiANEBmuEEEIIIYQQQgghDhAZrBFCCCGEEEIIIYQ4QGSwRgghhBBCCCGEEOIAkcEaIYQQQggh\nhBBCiANEBmuEEEIIIYQQQgghDpCBHKz5zu/8Tg3Ih3x046NvJLfy0cWPvpHcykcXP/pGcisfXfzo\nG8mtfHT5oy8kt/LR5Q9RYyAHa5aWlvb7FIRom+RWDCLJrRhEklsxiCS3YhBJboXonYEcrBFCCCGE\nEEIIIYQ4rGSwRgghhBBCCCGEEOIAkcEaIYQQQgghhBBCiANEBmuEEEIIIYQQQgghDhAZrNknVVeK\nXQshhBBCCCGEEGI7Y79P4Ch6c6nARz7xNzx9ZoTf/oeXUUrt9ykJceBoralmMriWhc808afT0lZE\nxyRPQuyNtCHRCcmNOGok86KbZLBmH/zRC7exKi5/fWOBb9zPcX4isd+nJMSBorXGunaN4pUruLk8\nvniMyOXLmBcvygVPtE3yJMTeSBsSnZDciKNGMi+6TZZB7YMv3Fzk4qQ3QPOX1+7v89kIcfBUMxnv\nQpfNgda42RzFK1eoZjL7fWpiAEmehNgbaUOiE5IbcdRI5kW3yWBNn5WdKq8t5Hn/20Y5MRzh2t3s\nfp+SEAeOa1m4ufzW13J5XMvapzMSg0zyJMTeSBsSnZDciKNGMi+6TQZr+uzW/TyOq7k4leD8RJwb\nd3P7fUpCHDg+08QXj219LR7DZ5r7dEZikEmehNgbaUOiE5IbcdRI5kW3yWBNn7224I22vm08zvmJ\nBG8uF7Aq1X0+KyEOFn86TeTyZXyJOCiFLxEncvky/nR6v09NDCDJkxB7I21IdEJyI44aybzoNikw\n3GezK0UAZlIRTo1E0dp77aGx+D6fmRAHh1IK8+JFAhMTUk1f7JnkSYi9kTYkOiG5EUeNZF50mwzW\n9NncaomRWJBw0M+xdBiAO5mSDNYIUUcphTE8vN+nIQ4JyZMQeyNtSHRCciOOGsm86CZZBtVnsysl\nplMRAI6t/3lnfbaNEEIIIYQQQgghhAzW9NnsSomZpDejZjQeImT4uJORwRohhBBCCCGEEEJ4ZLCm\nj7TW3FuzmBjyKoIrpZhOhplfk+3chBBCCCGEEEII4ZGaNX1UsKuUKlXG4qHN18YSIRayMlgjBFpD\nYQkqJQiEIToCUpBNHEaSdbHfJINCNCZtQ7RCciL6RAZr+mgxVwa85U8bJhImV2+v7NcpCXEwaA13\nvw5vPQtWFswEnHgaJh/b+8VPLqiim/aap15mXYhW9DqD0ueKQaU1zH8NXv9rL8PRETjzQZh6h2T4\nqKvt14JRWL0Nt5+T67joORms6aONGTRjcXPztfGEyf1sGa21bOsmjq7C0vobhzXvc2vN+zwxDbHR\nzr+vvDEW3dSNPPUq60K0qpcZlD5XDLLCIlz/tJdhpwxGCOw8DE1DbGy/z07sl/p+bfJRmH0R/AFA\nyXVc9JTUrOmjxfz2mTVjCRPbcVktVvbrtITYf5WSdwGsZWW91/diy5sS/eCCWlja2/cVR1M38tSr\nrAvRql5mUPpcMchKq3DvZXAsQHt/3nvZe10cXfX9mna9XNg1G8TIdVz0iAzW9NFCdvtgzXjC++/7\nOalbI44QrSG/CCu3vT+DUe8JbC0z4U2h3wt5Yyy6qVme6nOt9fbvEQj3JutCtKpRBlMnAHf37LZC\n+lzRTCv95H5RPgjVtY1QwntdHF31/VrV9nLhOg9ea+U6fpCzLw6sni+DUkp9J/AJwA98Smv9aw2O\n+XvALwMa+LrW+u/3+rz2Q6Zg4/cpkuHA5msjMW+wZilnw8R+nZkQfdRomvzxd8PpD8Abn9s6dT46\nsreftfGmZGO6P2y5oGqtqWYyuJaFzzTxp9OyHFEAO2Rjtzy1uvwjOuK9Xn/cXrMuRKvqM5g6AbFx\nuPGnYOX2tnRplzYi/a3oxTK5ruYqnIJzH4abn/WWREVHvc/Dqc6+nzgc6vu1wrKXi7U5qFa2Xccb\nZhJkiajoSE8Ha5RSfuC3gA8Bs8CLSqlPa62v1RxzFvhF4D1a6xWl1KFdFJop2qQiAXy+B41yc7Bm\nfYmUEIdeo3oJt5+Dt38fvP37u1uUcpc3xlprrGvXKF65gpvL44vHiFy+jHnxoryBOOJ2zMaFC6id\nBlparQOilHdzlpiWAqxif9RnEHd9oGb9yfFe6i/s0OfqyLD0t6Lr9ZK6fh2PpGHiMW/WhHa9GTWp\nU97r4uiq79fcipeTMx+EirXlOr5jJk9OoKRenehAr2fWPAm8prV+A0Ap9UfA9wDXao75MeC3tNYr\nAFrrhR6f077J5G3S0eCW10Zi3ucyWCOOjB2nyVuQOr75ktaa6vLy3p6W7fLGuLq87F1MszkA3GyO\n4pUrBCYmMIaH9/qvFANo42mYk82S/9u/Rds2CrU1GzsNtLSz/EMpuTkT+6s2gyu3vRk1tTpdurRD\nn1vNZDb7W43GuX+f/Oc/jz+RIDAzIwM2R0UL/WQ7M2VqcwVduI4rBWPnvX5dBtOPpB3z1+JDlh0z\nmfwWDFkiKjrQ68GaaeBOzeezwLvqjjkHoJT6Et5SqV/WWv9Z/TdSSv048OMAx48fr//rgeDNrNk6\nWDMUDhDwK5by9j6dleilw5DbrmuyNAm6/LRshzfGrmXh5vJbX8vlcS2pH3UUc1ubucD0tPfn5CTG\n6Kg3YLORjZ0GWlrIteito5jbruh2dhu0kY3+VqNxFhepzM+j7QrmI49QzWaP9AybI5XbFpYmt3Pt\n78l1XAbTW3IYc9s0fy3kYsdMVrTcI4iOHISKWQZwFng/8EPAv1NKJesP0lp/Umt9WWt9eXR0MDvR\nTGH7zBqlFMPREMsys+ZQOgy57bqN6aTmEKC8P+tqdmx5MqH15pOJaibTtdPwmSa+eGzra/EYPtPs\n2s8YVEcxt1ue/NsV/PG494ay5D31apqNFnIteuso5rYr+pDdjf5Wl0peuyrbGCPDuIVi1/v2QXOk\nctska+1e++U6vn8OY267ce+5YyZjQ3KPIDrS65k1c8Cxms9n1l+rNQs8r7WuAG8qpW7iDd682ONz\n67uVBoM1AMOxoCyDEkdHC9NJ+zHrxZ9OE7l8edsTFH9a1qYfRbWZc1ZWiD39HvLPfgldreJLxJtn\nQ2rRiEHVh+xu9Lf5z38ebVcwRkeIPf0enJUVmdF4lDTJWrvXfrmOi27qxr3njpkcHgaG5R5BtK3X\ngzUvAmeVUqfwBml+EKjf6emP8WbU/K5SagRvWdQbPT6vvnNdzUpxp8GaEMsFWQYljpAm00k3nkxs\nrPmF7j8tU0phXrxIYGJCdicRWzLnZjKQTpP4ru8idOoU/qGh1rIh0+fFoOpxdjf6W38igfnII7iF\nojdQk8ngS8RlJsRRskvW2r32y3VcdFM37j2bZlLuEUSberoMSmvtAD8DfBa4Dvx7rfWrSqmPKaU+\nun7YZ4FlpdQ14HPAz2utl3t5Xvsha1VwNdtq1gAMR4NkZLBGHCVaQ37RK2yZX/Q+r7HxZMKXiINS\nrc1s6IBSCmN4mOD0NMbwsNzgHWH1mcOpEJiYIHjq1N6y0STrQgycDjOtlCIwM4MxMoKzuIC7stKz\nvl0Mppau/XX5UyDXcdE
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa780527cf8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"fig = sns.pairplot(df,\n",
" vars=norm_matieres,\n",
" hue=\"Classe\",\n",
" diag_kind=\"kde\",\n",
" plot_kws={'alpha':0.5,},\n",
" )\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Le total des points"
]
},
{
"cell_type": "code",
"execution_count": 41,
"metadata": {
"collapsed": true,
"slideshow": {
"slide_type": "skip"
}
},
"outputs": [],
"source": [
"bp_data = df[[\"total\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1)\n",
"bp_data.columns = bp_data.columns.droplevel()"
]
},
{
"cell_type": "code",
"execution_count": 42,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa78013dbe0>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 42,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
2018-04-12 18:06:58 +00:00
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3EAAAE/CAYAAADouUp5AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+UXWd5H/rvcy0neGHH/DAZbAwWtCYdogSnaHFzLyZ3\nFLVcgltImpaiJASCiJO7wM29zbpGRG0MSbUi2qTcdjWlFSgL04ZxaCCEIuJCiSYsp4HUgAEnE4JN\n5YtsY/PLBiWua5unf8wRjIUsjTRndM6e+XzWOmvOefeP85y9X53Rd/a7967uDgAAAMPwv0y6AAAA\nAFZOiAMAABgQIQ4AAGBAhDgAAIABEeIAAAAGRIgDAAAYECEOgEGrqkdVVVfVxSucf29VvWWt6zrm\nPb+9qo5U1UVn8n0BWJ+EOADGbhRYjj6+XlX3LXv94ydZ9vlVdcuZqvVM6O77u/vc7r7jZPOeaigF\nYOPZNOkCAFh/uvvco8+r6lCSV3b3f55cRQCwfjgSB8AZV1XnVNWvV9WdVXW4qv5ZVZ1dVY9P8jtJ\nnrbsyN3jq+o5VfWRqrqnqu6oqjdW1Yr+EFlVf7Wq/rCqvlZVv5fkscdMf+6ydX+sqp5zgnV9vqqu\nrqo/q6ovV9W+qvr2ZdNfVVW3VtWXqupdVTUzan/Y0bWquq6q/r+q+k+juv6wqi4ZreZDo5+fHn3+\nH66qJ1bV9aMav1RVv7/ijQ3AuiPEATAJr0/yvUm+J8mzkswlubq7v5TkR5J8djT88NxR2wNJXp3k\n8Umem+RvJ3nlyd6kqirJf8hSMHp8kl9N8tJl0zcneXeS3Ukel+QfJXl3VT322HUtsyPJDyb5riTf\nl+T/Ha3rBUn+8aj+JyX5YpJ/d4L1/FiS147e987RNkmSHxj9/K7R5393ktck+XSSC5JcmOR1J/no\nAKxjQhwAk/DjSa7p7i92911J/kmWhatjdfcfd/d/7e6HuvvWJG9J8n+s4H0uTTKb5PXd/T+6+4NJ\nrl82/WVJ3tXd/7m7v97d70vyp0med4J1/ovuvqO7v5DkV7IU6o5+pn3d/cnu/u9Jrk7yN6rqiY+w\nnnd098e6+4Ekb09y2Qne84EkFyV5yuhzfOgE8wKwzglxAJxRo6NjT0xy27Lm27J09OqRlnlGVf1e\nVd1VVV9N8otZOip1Mhcl+cIoVC1/r6MuSfITo2GK91TVPUm2jpZ7JJ87Zl1H571o+bq7+54kXz3B\n5/r8sud/meTcR5gvSfYkuSPJwaq6par+4QnmBWCdE+IAOKO6u7MUYC5Z1vyUJLcfneU4i705yceS\n/JXu/o4kv5SkVvB2dya5oKoedcx7HfW5JG/p7scsezy6u994gnU++Zh1Hb3i5B1Z9pmq6jFJvmPZ\n51qpb/n83X1vd/9cd1+S5EeT/KMTnbsHwPomxAEwCfNJrhldtOQ7s3RO2r8fTbsryXdW1fIjU+cl\nube7j1TVdyf56RW+z59n6Vyyf1xV31ZV25I8f9n0a5P8varaXlVnjS64sv0EQyCT5B9U1YVVdUGS\nXUl+a9ln+umq2jIKjXuT/H53f/6RVnQ83X1/knuTPO1oW1W9sKqeNjqKeW+Sh5J8/VTWC8D6IcQB\nMAm/mKVzz/4kyU1J/jDJPx1N+0SS9yS5bTTE8XFJ/p8kr6yqI0l+Pd8MTic0Our34iTbknw5S+ep\n/ftl0z+bpSNbr8/ShUhuS/JzOfHvx+uSHEzymSSfOlp3d783S+fIvSdLR+WemBOc53cSv5jkP4w+\n/wuzdF7fwSRfy9JFWn61u//oNNcNwMDV0u83AOBkqurzSf5ud98w6VoA2LgciQMAABgQIQ4AAGBA\nDKcEAAAYEEfiAAAABkSIAwAAGJBNky4gSS644ILevHnzpMtYN/7iL/4ij370oyddBnwLfZNppn8y\nrfRNppn+OT4f/ehHv9jdT1jJvFMR4jZv3pwbb7xx0mWsGwsLC5mbm5t0GfAt9E2mmf7JtNI3mWb6\n5/hU1W0rnddwSgAAgAER4gAAAAZEiAMAABgQIQ4AAGBAhDgAAIABEeIAAAAGRIgDAAAYECEOAGAK\nzc/PZ8uWLdm+fXu2bNmS+fn5SZcETImpuNk3AADfND8/n927d2f//v156KGHctZZZ2Xnzp1Jkh07\ndky4OmDSHIkDAJgye/bsyf79+7Nt27Zs2rQp27Zty/79+7Nnz55JlwZMgZOGuKp6clUdrKo/rao/\nqaqfG7U/rqo+UFWfGf187Ki9qupfVtUtVfXJqvrra/0hAADWk8XFxVx++eUPa7v88suzuLg4oYqA\nabKSI3EPJvn57n5Gku9P8qqqekaSXUk+2N2XJvng6HWS/FCSS0ePK5O8aexVAwCsY7Ozs7nhhhse\n1nbDDTdkdnZ2QhUB0+SkIa677+zuj42efy3JYpInJXlRkmtHs12b5IdHz1+U5G295MNJHlNVF469\ncgCAdWr37t3ZuXNnDh48mAcffDAHDx7Mzp07s3v37kmXBkyBU7qwSVVtTvJ9ST6SZKa77xxN+nyS\nmdHzJyX53LLFDo/a7gwAACd19OIlV111VRYXFzM7O5s9e/a4qAmQJKnuXtmMVecm+YMke7r7XVV1\nT3c/Ztn0r3T3Y6vqvUn2dvcNo/YPJnlNd994zPquzNJwy8zMzDzruuuuG88nIkeOHMm555476TLg\nW+ibjMu2bdsmXcKKHTx4cNIlMHC+O5lm+uf4bNu27aPdvXUl867oSFxVnZ3knUl+s7vfNWq+q6ou\n7O47R8Ml7x61357kycsWv3jU9jDdvS/JviTZunVrz83NraQUVmBhYSG2J9NI32RcVvoHyFOxedeB\nHNp7xdjXC6vlu5Nppn9OxkquTllJ9idZ7O5/vmzSe5K8bPT8ZUl+d1n7T46uUvn9Se5dNuwSAACA\nVVjJkbjnJHlpkk9V1U2jtl9IsjfJO6pqZ5Lbkrx4NO19SV6Q5JYkf5nkp8ZaMQAAwAZ20hA3Oret\nHmHy9uPM30letcq6AAAAOI6V3CcOAACAKSHEAQAADIgQBwAAMCBCHAAAwIAIcQAAAAMixAEAAAyI\nEAcAADAgQhwAAMCACHEAAAADIsQBAAAMiBAHAAAwIEIcAADAgAhxAAAAAyLEAQAADIgQBwAAMCBC\nHAAAwIAIcQAAAAMixAEAAAyIEAcAADAgQhwAAMCACHEAAAADIsQBAAAMiBAHAAAwIEIcAADAgAhx\nAAAAA3LSEFdVv1FVd1fVzcvafquqbho9DlXVTaP2zVV137Jp/2YtiwcAANhoNq1gnrcm+VdJ3na0\nobv//tHnVfVrSe5dNv+t3X3ZuAoEAADgm04a4rr7Q1W1+XjTqqqSvDjJD463LAAAAI5ntefEPTfJ\nXd39mWVtT62qj1fVH1TVc1e5fgAAAJZZyXDKE9mRZH7Z6zuTPKW7v1RVz0ry7qr67u7+6rELVtWV\nSa5MkpmZmSwsLKyyFI46cuSI7clYbNu2bdIlrMjBgwcnXQLrhO9OppHf60wz/XMyTjvEVdWmJH8n\nybOOtnX3/UnuHz3/aFXdmuTpSW48dvnu3pdkX5Js3bq15+bmTrcUjrGwsBDbk3Ho7rGub/OuAzm0\n94qxrhPG5voDvjuZSn6vM830z8lYzXDKv5Hkz7r78NGGqnpCVZ01ev60JJcm+ezqSgQAAOColdxi\nYD7JHyX5rqo6XFU7R5NekocPpUySH0jyydEtB347yc9295fHWTAAAMBGtpKrU+54hPaXH6ftnUne\nufqyAAAAOJ7VXp0SAACAM0iIAwAAGBAhDgAAYECEOAAAgAER4gAAAAZEiAMAABiQk95iAACAlamq\nSZewYt096RKA0+RIHADAmHT32B+XvOa9a7JeYLiEOAAAgAER4gAAAAZEiAMAABgQIQ4AAGBAhDgA\nAIABEeIAAAAGRIgDAAAYECEOAABgQIQ4AACAARHiAAAABkSIAwAAGBAhDgAAYECEOAAAgAHZNOkC\ngPF45uvfn3vve2DSZZz
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa78af72dd8>"
]
},
"metadata": {},
"output_type": "display_data"
2018-04-10 11:22:39 +00:00
}
],
"source": [
2018-04-12 18:06:58 +00:00
"bp_data.plot(title=\"Total de points\",\n",
" kind=\"box\",\n",
" grid=True,\n",
" figsize=(15,5))"
2018-04-10 11:22:39 +00:00
]
},
{
2018-04-12 18:06:58 +00:00
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
2018-04-10 11:22:39 +00:00
"source": [
2018-04-12 18:06:58 +00:00
"## Français"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 43,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b68f400>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 43,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
2018-04-12 18:06:58 +00:00
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHRFJREFUeJzt3X+wnXddJ/D3x6SVCrFQitcudQgrFS+WKcpd/JVZb6gg\nWt3WGZYxOm50spN/tKPuuttoZkTGzWxwZlUcWd3MRjfjYCoi2NpooHZyxaKilB8CXrDAFi2UVqCU\nplulrd/94z6BS7jNPek9N8/z5LxeM2fOeZ7znPN8zvN8cnLf5/lVrbUAAAAwHF/WdwEAAAB8MUEN\nAABgYAQ1AACAgRHUAAAABkZQAwAAGBhBDQAAYGAENQAAgIER1AAAAAZGUAMAABiYredyZpdeemnb\nvn37uZzlee2hhx7Kk5/85L7LgC+hNxkqvcmQ6U+GSm9O1x133PHJ1toz1pvunAa17du35x3veMe5\nnOV5bWlpKYuLi32XAV9CbzJUepMh058Mld6crqr66CTTrbvrY1U9t6rever22ar6yaq6pKpurao7\nu/unbbxsAAAA1g1qrbUPttZe0Fp7QZIXJvl/Sd6UZF+S21prVyS5rRsGAABgg872ZCJXJ/lwa+2j\nSa5NcqQbfyTJddMsDAAAYFZVa23yiat+M8k7W2u/VlWfaa09tRtfSe4/NXzaa/Ym2Zskc3NzL7zx\nxhunUzk5efJknvKUp/RdBnwJvclQ6U2GTH8yVHpzunbu3HlHa21hvekmDmpVdWGSjyf5htbavauD\nWvf8/a21Mx6ntrCw0JxMZHoc2MlQ6U2GSm8yZPqTodKb01VVEwW1s9n18buzsjXt3m743qq6rJvZ\nZUnuO/syAQAAON3ZBLVdSY6uGr45ye7u8e4kN02rKAAAgFk2UVCrqicneUmSN64afTDJS6rqziTf\n2Q0DAACwQRNd8Lq19lCSp5827lNZOQskAAAAU3S2p+cHAABgk020RQ0AgC9YuTLROJzNpZiA4bBF\nDQDgLLXWpn571g23bMr7AuMkqAEAAAyMoAYAADAwghoAAMDACGoAAAADI6gBAAAMjKAGAAAwMIIa\nAADAwAhqAAAAAyOoAQAADIygBgAAMDCCGgAAwMAIagAAAAMjqAEAAAyMoAYAADAwghoAAMDACGoA\nAAADI6gBAAAMjKAGAAAwMIIaAADAwGztuwCgX1XVdwkTa631XQIAwDlhixrMuNba1G/PuuGWTXlf\nAIBZIagBAAAMjKAGAAAwMIIaAADAwAhqAAAAAzNRUKuqp1bVG6rqA1W1XFXfWlWXVNWtVXVnd/+0\nzS4WAABgFky6Re01SY631r4+yVVJlpPsS3Jba+2KJLd1wwAAAGzQukGtqi5O8m+THE6S1trnWmuf\nSXJtkiPdZEeSXLdZRQIAAMySSS54/ewk/5jkt6rqqiR3JPmJJHOttXu6aT6RZG6tF1fV3iR7k2Ru\nbi5LS0sbrZnOyZMnLU8GS28yRL43GTr9yRD57uzHJEFta5JvSnJ9a+3tVfWanLabY2utVdWaV6Nt\nrR1KcihJFhYW2uLi4sYq5vOWlpZieTJIx4/pTQbJ9yaD5ruTgfLd2Y9JjlG7O8ndrbW3d8NvyEpw\nu7eqLkuS7v6+zSkRAABgtqwb1Fprn0jyD1X13G7U1Un+NsnNSXZ343YnuWlTKgQAAJgxk+z6mCTX\nJ3ldVV2Y5CNJfjQrIe/1VbUnyUeTvGJzSgQAAJgtEwW11tq7kyys8dTV0y0HAACASa+jBgAAwDki\nqAEAAAyMoAYAADAwghoAAMDACGoAAAADI6gBAAAMjKAGAAAwMIIaAADAwAhqAAAAAyOoAQAADIyg\nBgAAMDCCGgAAwMBs7bsAAABgOqqq7xIm1lrru4RBs0UNAADOE621qd+edcMtm/K+nJmgBgAAMDCC\nGgAAwMA4Rg2AQXKcBQCzzBY1AAbJcRYAzDJBDQAAYGAENQAAgIER1AAAAAZGUAMAABgYZ30EAM5r\nV73qLXng4Uf6LmMi2/cd67uEdV180QV5zytf2ncZcN4T1ACA89oDDz+Suw5e03cZ61paWsri4mLf\nZaxrDGESzgd2fQQAABgYQQ0AAGBgBDUAAICBmegYtaq6K8mDSR5L8mhrbaGqLknyu0m2J7krySta\na/dvTpkAAACz42y2qO1srb2gtbbQDe9Lcltr7Yokt3XDAAAAbNBGdn28NsmR7vGRJNdtvBwAAAAm\nDWotyVuq6o6q2tuNm2ut3dM9/kSSualXBwAAMIMmvY7ajtbax6rqq5LcWlUfWP1ka61VVVvrhV2w\n25skc3NzWVpa2ki9rHLy5EnLk8HSmwyV3pxNY1jvY/p/fSx1Mj3W+bk3UVBrrX2su7+vqt6U5EVJ\n7q2qy1pr91TVZUnue5zXHkpyKEkWFhbaGC7kOBZjuTAmM+j4Mb3JMOnN2TSS9T6a/9dHsjyZIuu8\nF+vu+lhVT66qbaceJ3lpkvcluTnJ7m6y3Ulu2qwiAQAAZskkW9Tmkrypqk5N/zutteNV9ddJXl9V\ne5J8NMkrNq9MAACA2bFuUGutfSTJVWuM/1SSqzejKAAAgFm2kdPzAwAAsAkENQAAgIER1AAAAAZG\nUAMAABgYQQ0AAGBgBDUAAICBEdQAAAAGRlADAAAYGEENAABgYAQ1AACAgRHUAAAABkZQAwAAGBhB\nDQAAYGAENQAAgIER1AAAAAZGUAMAABgYQQ0AAGBgBDUAAICBEdQAAAAGRlADAAAYGEENAABgYAQ1\nAACAgdnadwEAAJtp2/y+PP/Ivr7LmMyRvgtY37b5JLmm7zLgvCeoAQDntQeXD+aug8MPFktLS1lc\nXOy7jHVt33es7xJgJtj1EQAAYGAENQAAgIER1AAAAAZGUAMAABiYiYNaVW2pqndV1S3d8LOr6u1V\n9aGq+t2qunDzygQAAJgdZ7NF7SeSLK8afnWSX26tPSfJ/Un2TLMwAACAWTXR6fmr6vKsXDDjQJL/\nVFWV5MVJfrCb5EiSn0/y65tQI9C56lVvyQMPP9J3GRMZw+mbL77ogrznlS/tuwwAgC8x6XXUfiXJ\nf02yrRt+epLPtNYe7YbvTvLMKdcGnOaBhx9xLaApGkOYBABm07pBraq+N8l9rbU7qmrxbGdQVXuT\n7E2Subm5LC0tne1b8DhOnjxpec6gMazzMfXmWOpkeqzz2TSG9e67kyGzzs+9SbaofXuSf1dV35Pk\nSUm+Mslrkjy1qrZ2W9UuT/KxtV7cWjuU5FCSLCwstDH8yj4WY9lqwRQdPzaKdT6a3hzJ8hyDMe2W\n+yPHH+q7hHXZLXfKRvJv3Xcng2Wd92LdoNZa+5kkP5Mk3Ra1n26t/VBV/V6Slye5McnuJDdtYp0A\nDJjdcqfLbrkAbOQ6ajdk5cQiH8rKMWuHp1MSAADAbJv0ZCJJktbaUpKl7vFHkrxo+iUBAADMtrMK\nagAAwHSM6fjeMeySfb4d3yuoAQBADxzfO11jCJNnYyPHqAEAALAJBDUAAICBEdQAAAAGRlADAAAY\nGEENAABgYAQ1AACAgRHUAAAABkZQAwAAGBhBDQAAYGAENQAAgIHZ2ncBAACbbfu+Y32XMJnjw6/z\n4osu6LsEmAmCGgBwXrvr4DV9lzCR7fuOjaZWYPPZ9XGEjh49miuvvDJXX311rrzyyhw9erTvkgAA\ngCmyRW1kjh49mv379+fw4cN57LHHsmXLluzZsydJsmvXrp6rAwAApsEWtZE5cOBADh8+nJ07d2br\n1q3ZuXNnDh8+nAMHDvRdGgAAMCWC2sgsLy9nx44dXzRux44dWV5e7qkiAABg2gS1kZmfn8/tt9/+\nReNuv/32zM/P91QRAAAwbYLayOzfvz979uzJiRMn8uijj+bEiRPZs2dP9u/f33dpAADAlDiZyMic\nOmHI9ddfn+Xl5czPz+fAgQNOJAIAAOcRQW2Edu3alV27dmVpaSmLi4t9lwMAAEyZXR8BAAAGRlAD\nAAAYGEENAABgYAQ1AAC
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa77b683390>"
]
},
"metadata": {},
"output_type": "display_data"
2018-04-10 11:22:39 +00:00
}
],
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"Français\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Histoire géo"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 44,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b4f8710>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 44,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
2018-04-12 18:06:58 +00:00
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAGGtJREFUeJzt3X+wpXddH/D3RzZAJomAhl4jUlaFahiRoLcMFh0uQSgV\np8DUOqUdwOp0pdUWLLTs4FS01ula+dHaOtR14hA7VOrwQ2gWI5jmSu0oNcEAgTAj0tBCAxGBkBtT\nmoRP/7jP0suyyT3ZPWfP99zzes2c2Xuen5/7nM89d9/3ec73qe4OAAAA4/iqZRcAAADAlxPUAAAA\nBiOoAQAADEZQAwAAGIygBgAAMBhBDQAAYDCCGgAAwGAENQAAgMEIagAAAIM5dC53dvHFF/fhw4fP\n5S4PtDvuuCMXXHDBssuAr6A3GZXeZGT6k1Hpzfm6/vrrP93dD99vuX2DWlU9OMm7kzxoWv5N3f3K\nqnp9kqckuW1a9Ie6+4b72tbhw4dz3XXX7bdLZrS9vZ2tra1llwFfQW8yKr3JyPQno9Kb81VVH5tl\nuVnOqH0hyeXdvVNV5yX5var6rWneP+nuN51pkQAAAHylfYNad3eSnenpedOjF1kUAADAOptpMJGq\nekBV3ZDk1iTv6u73TLN+rqreX1WvraoHLaxKAACANVK7J8xmXLjqoUnemuQfJvmzJJ9M8sAkx5P8\nSXf/89OscyTJkSTZ2Nj4zje+8Y1zKJsk2dnZyYUXXrjsMuAr6E1GpTcZmf5kVHpzvp761Kde392b\n+y13v4JaklTVTyX58+5+1Z5pW0le1t3ff1/rbm5utsFE5scHOxmV3mRUepOR6U9GpTfnq6pmCmr7\nXvpYVQ+fzqSlqs5P8vQkH66qS6ZpleQ5SW48u5IBAABIZhv18ZIkV1bVA7Ib7H6ju6+qqv9SVQ9P\nUkluSPKiBdYJAACwNmYZ9fH9SZ5wmumXL6QiAACANTfTqI8AAACcO4IaAADAYGb5jBoALMXueFXj\nu78jKAPAfpxRA2BY3T3Xx6NeftXctymkAbAIghoAAMBgBDUAAIDBCGoAAACDEdQAAAAGI6gBAAAM\nRlADAAAYjKAGAAAwGEENAABgMIIaAADAYAQ1AACAwQhqAAAAgxHUAAAABiOoAQAADEZQAwAAGMyh\nZRcAALBqqmrZJcysu5ddAnAGnFEDALifunvuj0e9/KqFbBdYTYIaAADAYAQ1AACAwQhqAAAAgxHU\nAAAABiOoAQAADEZQAwAAGIygBgAAMBhBDQAAYDCCGgAAwGAENQAAgMHsG9Sq6sFV9d+r6n1V9cGq\n+plp+jdW1Xuq6iNV9Z+q6oGLLxcAAODgm+WM2heSXN7dj09yWZJnVtWTkvx8ktd296OTfDbJjyyu\nTAAAgPWxb1DrXTvT0/OmRye5PMmbpulXJnnOQioEAABYM4dmWaiqHpDk+iSPTvJLSf4kyee6++5p\nkY8necS9rHskyZEk2djYyPb29lmWzEk7OzuOJ0PSm4xMbzIy/cmI/F5fjpmCWnffk+Syqnpokrcm\n+dZZd9Ddx5McT5LNzc3e2to6gzI5ne3t7TiejEhvMqyrT+hNxqU/GZTf68txv0Z97O7PJbk2yXcl\neWhVnQx635DkE3OuDQAAYC3NMurjw6czaamq85M8PclN2Q1sPzAt9sIkb1tUkQAAAOtklksfL0ly\n5fQ5ta9K8hvdfVVVfSjJG6vqXyT5oyRXLLBOAACAtbFvUOvu9yd5wmmmfzTJExdRFAAAwDq7X59R\nAwAAYPEENQAAgMHMNDw/cHBV1bJLmFl3L7sEABia3+sHhzNqsOa6e+6PR738qoVsFwC4b36vHxyC\nGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEAAAxGUAMAABiMoAYAADAYQQ0AAGAwghoAAMBgBDUA\nAIDBCGoAAACDEdQAAAAGI6gBAAAMRlADAAAYjKAGAAAwGEENAABgMIIaAADAYA4tuwAAgEV6/M+8\nM7fdedeyy5jJ4aMnll3Cvh5y/nl53yufsewy4MAT1ACAA+22O+/Kzceetewy9rW9vZ2tra1ll7Gv\nVQiTcBC49BEAAGAwghoAAMBgBDUAAIDBCGoAAACDEdQAAAAGI6gBAAAMRlADAAAYzL5BraoeWVXX\nVtWHquqDVfXiafpPV9UnquqG6fF9iy8XAADg4Jvlhtd3J3lpd7+3qi5Kcn1VvWua99ruftXiygMA\nAFg/+wa17r4lyS3T17dX1U1JHrHowgAAANbVLGfUvqSqDid5QpL3JHlykh+vqhckuS67Z90+e5p1\njiQ5kiQbGxvZ3t4+u4r5kp2dHceTYelNRqU319MqvO6r9Ht9Vepkfrzm597MQa2qLkzy5iQv6e7P\nV9Xrkvxskp7+fXWSHz51ve4+nuR4kmxubvbW1tYcyibZ/YFxPBnS1Sf0JmPSm+tpRV73lfm9viLH\nkznymi/FTKM+VtV52Q1pb+jutyRJd3+qu+/p7i8m+ZUkT1xcmQAAAOtjllEfK8kVSW7q7tfsmX7J\nnsWem+TG+ZcHAACwfma59PHJSZ6f5ANVdcM07RVJnldVl2X30sebk/zoQioEAABYM7OM+vh7Seo0\ns94x/3IAAACY6TNqAAAAnDuCGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEAAAxGUAMAABiMoAYA\nADAYQQ0AAGAwghoAAMBgBDUAAIDBCGoAAACDEdQAAAAGI6gBAAAMRlADAAAYjKAGAAAwGEENAABg\nMIeWXcC6qKpllzCz7l52CQAAsNacUTtHunvuj0e9/KqFbBcAAFguQQ0AAGAwghoAAMBgBDUAAIDB\nCGoAAACDEdQAAAAGI6gBAAAMxn3UAJiLx//MO3PbnXctu4x9HT56Ytkl7Osh55+X973yGcsu48C4\n6NKjedyVR5ddxmyuXHYB+7vo0iR51rLLgANPUANgLm67867cfGzs/7xtb29na2tr2WXsaxXC5Cq5\n/aZjw/dmoj+BL+fSRwAAgMEIagAAAIPZN6hV1SOr6tqq+lBVfbCqXjxN/5qqeldV/fH078MWXy4A\nAMDBN8sZtbuTvLS7H5vkSUl+rKoem+Rokmu6+zFJrpmeAwAAcJb2HUyku29Jcsv09e1VdVOSRyR5\ndpKtabErk2wneflCqgQAgANmVUbLTVZjEJmDNmLu/Rr1saoOJ3lCkvck2ZhCXJJ8MsnGvaxzJMmR\nJNnY2Mj29vYZlsrpOJ6MSm+up9Ff952dneFrPGlV6lwVq3A89ef6ue3Ou/L6Z16w7DL2tbOzkwsv\nvHDZZezrh66+40D15sxBraouTPLmJC/p7s9X1ZfmdXdXVZ9uve4+nuR4kmxubvYqDDu7Mq4+sRLD\n+LKG9OZ6WoHXfVWGP1+FY7lSVuR46s81tCLHUm8ux0yjPlbVedkNaW/o7rdMkz9VVZdM8y9Jcuti\nSgQAAFgvs4z6WEmuSHJTd79mz6y3J3nh9PULk7xt/uUBAACsn1kufXxykucn+UBV3TBNe0WSY0l+\no6p+JMnHkvzgYkoEAABYL7OM+vh7SepeZj9tvuUAAAAw02fUAAAAOHcENQAAgMHcr/uoAcvlxpjz\nddBujAkAHByCGqyQ2+68Kzcfe9ayy9jXqtxvZRXCJACwnlz6CAAAMBhBDQAAYDCCGgAAwGAENQAA\ngMEIagAAAIMR1AAAAAZjeH4A4MBbmdtxXD1+nQ85/7xllwBrQVADAA60Vbj/ZLIbJlelVmDxXPoI\nAAAwGEENAABgMIIaAADAYAQ1AACAwQhqAAAAgxHUAAAABiOoAQAADEZQAwAAGIygBgAAMBhBDQAA\nYDCCGgAAwGAENQAAgMEIagAAAIMR1AAAAAYjqAEAAAxGUAMAABiMoAYAADCYQ8suAAAA1tFFlx7N\n4648uuwyZnPlsgvY30WXJsmzll3G3Owb1KrqV5N8f5Jbu/vbpmk/neTvJfnTabFXdPc7FlUkAAAc\nNLffdCw3Hxs/WGxvb2d
2018-04-10 11:22:39 +00:00
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.figure.Figure at 0x7fa78990c630>"
2018-04-10 11:22:39 +00:00
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"HG\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Les maths"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 45,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b548588>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 45,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
2018-04-12 18:06:58 +00:00
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA2oAAAEyCAYAAACLaSO4AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHnZJREFUeJzt3X2QpWdZJ+Df7UyQmCDha9sIyOCC2DgYkF4KZdTuDFAq\nrom1iIxf0e2q2a3dHQW/mLVrF6i1q8LqiqhbruM2y7CmOiCCiURDcOxWp1aiCQQJtFtgDJgYEj8S\nYCCrmeHZP/od6Exm0j3p03Pec/q6qrq6z/t17jnn7jP9O+/zPqdaawEAAKA/vmTYBQAAAPBgghoA\nAEDPCGoAAAA9I6gBAAD0jKAGAADQM4IaAABAzwhqAAAAPSOoAQAA9IygBgAA0DM7z+WdPfGJT2y7\ndu06l3c51j772c/mggsuGHYZ8BB6k77Sm/SZ/qSv9OZg3XzzzX/XWnvSetud06C2a9eu3HTTTefy\nLsfa8vJypqenh10GPITepK/0Jn2mP+krvTlYVfXxjWxn6CMAAEDPCGoAAAA9I6gBAAD0jKAGAADQ\nM4IaAABAzwhqAAAAPSOoAQAA9IygBsDYW1xczO7du7N3797s3r07i4uLwy4JAB7WOf3AawA41xYX\nFzM3N5eFhYWcOHEiO3bsyOzsbJJk3759Q64OAE7PGTUAxtr8/HwWFhYyMzOTnTt3ZmZmJgsLC5mf\nnx92aQBwRhsKalX16qr6cFXdWlWLVfXoqnp6Vd1YVR+rqrdV1aO2ulgAOFsrKyvZs2fPg5bt2bMn\nKysrQ6oIANa3blCrqicn+dEkU6213Ul2JHllkjckeWNr7RlJ7k0yu5WFAsAjMTk5maNHjz5o2dGj\nRzM5OTmkigBgfRsd+rgzyflVtTPJlyW5K8mlSd7RrT+c5PLBlwcAmzM3N5fZ2dksLS3l+PHjWVpa\nyuzsbObm5oZdGgCc0bqTibTW7qyqn0/yiST3J7khyc1J7mutHe82uyPJk7esSgB4hE5OGHLgwIGs\nrKxkcnIy8/PzJhIBoNeqtfbwG1Q9LslvJfneJPcl+c2snkl7XTfsMVX11CS/1w2NPHX//Un2J8nE\nxMTzr7766oH+A7azY8eO5cILLxx2GfAQepO+0pv0mf6kr/TmYM3MzNzcWptab7uNTM//4iR/1Vr7\n2ySpqncmeVGSi6pqZ3dW7SlJ7jzdzq21Q0kOJcnU1FSbnp7e2L+AdS0vL8fjSR/pTfpKb9Jn+pO+\n0pvDsZFr1D6R5IVV9WVVVUn2JvlIkqUkL++2uSLJNVtTIgAAwPayblBrrd2Y1aGO70/yoW6fQ0le\nk+THq+pjSZ6QZGEL6wQAANg2NjL0Ma211yZ57SmLb0vygoFXBAAAsM1tdHp+AAAAzhFBDQAAoGcE\nNQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlADAADoGUENAACgZwQ1AACAnhHU\nAAAAekZQAwAA6BlBDQAAoGcENQAAgJ4R1AAAAHpGUAMAAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlAD\nAADoGUENAACgZwQ1AACAnhHUAAAAembdoFZVz6qqW9Z8fbqqXlVVj6+q91bVR7vvjzsXBQMAAIy7\ndYNaa+3/ttae21p7bpLnJ/lcknclOZjkSGvtmUmOdLcBAADYpLMd+rg3yV+21j6e5LIkh7vlh5Nc\nPsjCAAAAtqtqrW1846o3J3l/a+1Xquq+1tpF3fJKcu/J26fssz/J/iSZmJh4/tVXXz2YysmxY8dy\n4YUXDrsMRtzMzMywS9iwpaWlYZfAiPO6SZ/pT/pKbw7WzMzMza21qfW223BQq6pHJfmbJF/XWrt7\nbVDr1t/bWnvY69SmpqbaTTfdtKH7Y33Ly8uZnp4edhnwELsOXpfbr3zZsMuAh/C6SZ/pT/pKbw5W\nVW0oqJ3N0Mdvz+rZtLu723dX1cXdnV2c5J6zLxMAAIBTnU1Q25dkcc3ta5Nc0f18RZJrBlUUAADA\ndrahoFZVFyR5SZJ3rll8ZZKXVNVHk7y4uw0AAMAm7dzIRq21zyZ5winL/j6rs0ACAAAwQGc7PT8A\nAABbTFADAADoGUENAACgZwQ1AACAnhHUAAAAekZQAwAA6BlBDQAAoGcENQAAgJ4R1AAAAHpGUAMA\nAOgZQQ0AAKBnBDUAAICeEdQAAAB6RlADAADoGUENAACgZwQ1AACAnhHUAAAAekZQAwAA6BlBDQAA\noGcENQAAgJ4R1AAAhmhxcTG7d+/O3r17s3v37iwuLg67JKAHdg67AACA7WpxcTFzc3NZWFjIiRMn\nsmPHjszOziZJ9u3bN+TqgGFyRg0AYEjm5+ezsLCQmZmZ7Ny5MzMzM1lYWMj8/PywSwOGbENBraou\nqqp3VNVfVNVKVX1jVT2+qt5bVR/tvj9uq4sFABgnKysr2bNnz4OW7dmzJysrK0OqCOiLjZ5Re1OS\n61trX5vkkiQrSQ4mOdJae2aSI91tAAA2aHJyMkePHn3QsqNHj2ZycnJIFQF9sW5Qq6rHJvmWJAtJ\n0lr7p9bafUkuS3K42+xwksu3qkgAgHE0NzeX2dnZLC0t5fjx41laWsrs7Gzm5uaGXRowZBuZTOTp\nSf42yf+qqkuS3Jzkx5JMtNbu6rb5ZJKJrSkRAGA8nZww5MCBA1lZWcnk5GTm5+dNJAKkWmsPv0HV\nVJL3JXlRa+3GqnpTkk8nOdBau2jNdve21h5ynVpV7U+yP0kmJiaef/XVVw+y/m3t2LFjufDCC4dd\nBjzED1//2bzl2y4YdhnwEF436TP9SV/pzcGamZm5ubU2td52GzmjdkeSO1prN3a335HV69HurqqL\nW2t3VdXFSe453c6ttUNJDiXJ1NRUm56e3kj9bMDy8nI8nvTS9dfpTXrJ6yZ9pj/pK705HOteo9Za\n+2SSv66qZ3WL9ib5SJJrk1zRLbsiyTVbUiEAAMA2s9EPvD6Q5KqqelSS25L8SFZD3turajbJx5O8\nYmtKBAAA2F42FNRaa7ckOd04yr2DLQcAAICNfo4aAAAA54igBgAA0DOCGgAAQM8IagAAAD0jqAEA\nAPSMoAYAANAzghoAAEDPCGoAAAA9I6gBAAD0jKAGAADQM4IaAABAzwhqAAAAPSOoAQAA9IygBgAA\n0DOCGgAAQM8IagAAAD0jqAEAAPSMoAYAANAzghoAAEDPCGoAAAA9I6gBAAD0jKAGAADQM4IaAABA\nzwhqAAAAPbNzIxtV1e1JPpPkRJLjrbWpqnp8krcl2ZXk9iSvaK3duzVlAgAAbB9nc0ZtprX23Nba\nVHf7YJIjrbVnJjnS3QYAAGCTNjP08bIkh7ufDye5fPPlAAAAsKGhj0lakhuqqiX5tdbaoSQTrbW7\nuvWfTDJxuh2ran+S/UkyMTGR5eXlzVVMjhw5kt/4jd/IJz7xiXzVV31VfuAHfiB79+4ddlnwIH7X\n6aNjx47pTXpLf9JXenM4NhrU9rTW7qyqf5bkvVX1F2tXttZaF+Ieogt1h5JkamqqTU9Pb6bebW9x\ncTFXXXVV3vzmN+fEiRPZsWNHZmdn8+xnPzv79u0bdnmw6vrr4nedPlpeXtab9Jb+pK/05nBsaOhj\na+3O7vs9Sd6V5AVJ7q6qi5Ok+37PVhXJF83Pz2dhYSEzMzPZuXNnZmZmsrCwkPn5+WGXBgAADMi6\nQa2qLqiqx5z8OclLk9ya5NokV3SbXZHkmq0qki9aWVnJnj17HrRsz549WVlZGVJFAADAoG3kjNpE\nkqNV9cEkf5rkutba9UmuTPKSqvpokhd3t9lik5OTOXr06IOWHT16NJOTk0OqCKD/FhcXs3v37uzd\nuze7d+/O4uLisEsCgIe17jVqrbXbklxymuV/n8QMFufY3NxcZmdns7CwkBMnTmRpaSmzs7OGPgKc\nweLiYubm5r7wunny2t4kru0FoLc2OpkIPXHyj4oDBw5kZWUlk5OTmZ+f98cGwBmsvbb35AXxCwsL\nOXDggNdOAHprM5+jxpD
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa77b405c88>"
]
},
"metadata": {},
"output_type": "display_data"
2018-04-10 11:22:39 +00:00
}
],
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"Maths\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## SVT"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 46,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b2e9898>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 46,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
2018-04-12 18:06:58 +00:00
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3QAAAEyCAYAAACyDpLjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHGdJREFUeJzt3X2QZXdZJ/DvQyZoHMbwEmhDQBrLgKGMAWyDrogdwYgJ\nCu6ySqQ0vtWoi1W+4EqzVhnR2q2hXNnSjWUcTWTY0sAWGsw6cUg2m2tkF5Qkm4QJQROpQRIC2RAM\nmZBdE/jtH31Gmkl3utP3Tu79dX8+Vbf6vPzOOc+cfuZ2f/uce2+11gIAAEB/njDtAgAAANgcgQ4A\nAKBTAh0AAECnBDoAAIBOCXQAAACdEugAAAA6JdABAAB0SqADAADolEAHAADQqR3TLmA1J510Upuf\nn592GVvCAw88kJ07d067DFiV/mRW6U1mld5klunPybr++uvvaa09fb1xMxno5ufnc9111027jC1h\nNBplcXFx2mXAqvQns0pvMqv0JrNMf05WVX1sI+PccgkAANApgQ4AAKBTAh0AAECnBDoAAIBOCXQA\nAACdEugAAAA6JdABAAB0at1AV1XPrqprqurDVXVLVf3ssPypVXVVVd02fH3KGtufP4y5rarOn/Q/\nAAAAYLvayBW6h5O8sbX2giTfnOQNVfWCJEtJrm6tnZrk6mH+S1TVU5NckOQlSc5McsFawQ8AAIDH\nZt1A11q7q7V2wzB9f5Jbk5yS5NVJ9g3D9iV5zSqbf1eSq1pr97bWPpPkqiSvnEThAAAA292OxzK4\nquaTvCjJXyeZa63dNaz6ZJK5VTY5JcnHV8zfMSxbbd+7k+xOkrm5uYxGo8dSGms4fPiwc8nM0p/M\nKr3JpJx11lnTLmFDrrnmmmmXwBbguXM6NhzoqupJSf4kyc+11j5bVf+8rrXWqqqNU0hrbW+SvUmy\nsLDQFhcXx9kdg9FoFOeSWaU/mVV6k0lpbaxfjx5hfml/Du05d6L7hEnx3DkdG3qXy6o6Psth7o9a\na386LP5UVZ08rD85yd2rbHpnkmevmH/WsAwAAIAxbeRdLivJxUluba29bcWqy5McedfK85P82Sqb\nvzfJ2VX1lOHNUM4elgEAADCmjVyh+9YkP5TkO6rqxuFxTpI9Sb6zqm5L8ophPlW1UFV/kCSttXuT\n/HqSDw6PXxuWAQAAMKZ1X0PXWntfklpj9ctXGX9dkp9YMX9Jkks2WyAAAACr29Br6AAAAJg9Ah0A\nAECnBDoAAIBOCXQAAACdEugAAAA6JdABAAB0SqADAADolEAHAADQKYEOAACgUwIdAABApwQ6AACA\nTgl0AAAAnRLoAAAAOiXQAQAAdEqgAwAA6JRABwAA0Kkd0y4AAMZRVdMuYcNaa9MuAYAtxhU6ALrW\nWpv44zlv+vNjsl8AmDSBDgAAoFMCHQAAQKcEOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiU\nQAcAANCpHesNqKpLkrwqyd2tta8flr0ryfOHIU9O8o+ttReusu2hJPcn+XySh1trCxOqGwAAYNtb\nN9AleXuSC5O848iC1toPHJmuqt9Mct+jbH9Wa+2ezRYIAADA6tYNdK21a6tqfrV1VVVJvj/Jd0y2\nLAAAANYz7mvovi3Jp1prt62xviW5sqqur6rdYx4LAACAFTZyy+WjOS/JpY+y/qWttTur6hlJrqqq\nj7TWrl1t4BD4difJ3NxcRqPRmKWRJIcPH3YumVn6k1mmN5lVepNZ5ef6dGw60FXVjiT/Msk3rjWm\ntXbn8PXuqrosyZlJVg10rbW9SfYmycLCQltcXNxsaawwGo3iXDKr9Ccz68B+vcls0pvMMD/Xp2Oc\nWy5fkeQjrbU7VltZVTurateR6SRnJzk4xvEAAABYYd1AV1WXJnl/kudX1R1V9ePDqtflqNstq+qZ\nVXXFMDuX5H1VdVOSv0myv7V2YHKlAwAAbG8beZfL89ZY/iOrLPtEknOG6Y8mOWPM+gAAAFjDuO9y\nCQAAwJQIdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiUQAcAANApgQ4AAKBTAh0AAECnBDoAAIBO7Zh2\nAUAfqmraJWxYa23aJQAdOuMtV+a+Bx+adhnrml/aP+0S1nXiCcfnpgvOnnYZPAo/17cOgQ7YkGPx\nZDq/tD+H9pw78f0CbMZ9Dz40889Jo9Eoi4uL0y5jXT2Ezu3Oz/Wtwy2XAAAAnRLoAAAAOiXQAQAA\ndEqgAwAA6JRABwAA0CmBDgAAoFMCHQAAQKcEOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiU\nQAcAANApgQ4AAKBTAh0AAECnBDoAAIBOrRvoquqSqrq7qg6uWParVXVnVd04PM5ZY9tXVtXfVtXt\nVbU0ycIBAAC2u41coXt7kleusvw/tdZeODyuOHplVR2X5HeSfHeSFyQ5r6peME6xAAAAfNG6ga61\ndm2Sezex7zOT3N5a+2hr7Z+SvDPJqzexHwAAAFaxY4xtf6aqfjjJdUne2Fr7zFHrT0ny8RXzdyR5\nyVo7q6rdSXYnydzcXEaj0RilccThw4edS2aa/mRW6c3tada/7z39XO+lTibL9/3xt9lA97tJfj1J\nG77+ZpIfG6eQ1treJHuTZGFhoS0uLo6zOwaj0SjOJTPrwH79yWzSm9tTB9/3bn6ud3AuOQZ836di\nU+9y2Vr7VGvt8621LyT5/SzfXnm0O5M8e8X8s4ZlAAAATMCmAl1Vnbxi9vuSHFxl2AeTnFpVz62q\nJyZ5XZLLN3M8AAAAHmndWy6r6tIki0lOqqo7klyQZLGqXpjlWy4PJfnJYewzk/xBa+2c1trDVfUz\nSd6b5Lgkl7TWbjkm/woAAIBtaN1A11o7b5XFF68x9hNJzlkxf0WSR3ykAQAAAOPb1C2XAAAATJ9A\nBwAA0CmBDgAAoFMCHQAAQKcEOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRq3Q8WBwDYDnadtpTT9y1N\nu4z17Zt2AevbdVqSnDvtMmBbEOgAAJLcf+ueHNoz2yFkNBplcXFx2mWsa35p/7RLgG3DLZcAAACd\nEugAAAA6JdABAAB0SqADAADolEAHAADQKYEOAACgUwIdAABApwQ6AACATgl0AAAAnRLoAAAAOiXQ\nAQAAdEqgAwAA6JRABwAA0CmBDgAAoFMCHQAAQKcEOgAAgE6tG+iq6pKquruqDq5Y9htV9ZGqurmq\nLquqJ6+x7aGq+lBV3VhV102ycAAAgO1uxwbGvD3JhUnesWLZVUne3Fp7uKremuTNSd60xvZntdbu\nGatKAADYps54y5W578GHpl3Ghswv7Z92Ces68YTjc9MFZ0+7jIlZN9C11q6tqvmjll25YvYDSV47\n2bIAAIAkue/Bh3Joz7nTLmNdo9Eoi4uL0y5jXT2EzsdiI1fo1vNjSd61xrqW5Mqqakl+r7W2d62d\nVNXuJLuTZG5uLqPRaAKlcfjwYeeSmaY/t5c3XP1AHujjj8xd/MDfeXzyOy/fOe0ytpRZf07q6ed6\nL3X2oofzqT+nY6xAV1W/nOThJH+0xpCXttburKpnJLmqqj7SWrt2tYFD2NubJAsLC62HdN+DXv5S\nwjZ1YL/+3GYeOLDfX5knaH7J/6GJ6uA5qZfe7OFcdqWT86k/p2PT73JZVT+S5FVJXt9aa6uNaa3d\nOXy9O8llSc7c7PEAAAD4UpsKdFX1yiS/lOR7W2ufW2PMzqradWQ6ydlJDq42FgAAgMduIx9bcGmS\n9yd5flXdUVU/nuV3vdyV5dsob6yqi4axz6yqK4ZN55K8r6puSvI3Sfa31g4ck38FAADANrSRd7k8\nb5XFF68x9hNJzhmmP5rkjLGqAwAAYE2bfg0dAAAA0yXQAQAAdEqgAwAA6JRABwAA0CmBDgAAoFPr\nvsslAMB2Mb+0f9olrO/A7Nd44gnHT7sE2DYEOgCAJIf2nDvtEtY1v7S/izqBx49bLgEAADol0AEA\nAHRKoAMAAOiUQAcAANA
2018-04-10 11:22:39 +00:00
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.figure.Figure at 0x7fa77b328208>"
2018-04-10 11:22:39 +00:00
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"SVT\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Physique"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 47,
2018-04-10 11:22:39 +00:00
"metadata": {
2018-04-12 18:06:58 +00:00
"slideshow": {
"slide_type": "fragment"
}
2018-04-10 11:22:39 +00:00
},
2018-04-12 18:06:58 +00:00
"outputs": [
{
"data": {
"text/plain": [
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b19f358>"
]
},
"execution_count": 47,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3QAAAEyCAYAAACyDpLjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3X+0XWd5H/jvE8mRqXH4EQcFjGs1DSXSMoEkKiHFnVxh\nIMTQknYxKZomIY1qVV1EDXFYtWJlQptUs6TpxNPGZFXIkYNpqchqiROKHGPXS6fEM5BgXBOERQOh\nZrBx8KQQYxlbg8U7f9wtcy1f+V7fe6RzXt3PZ62z7jl777P3c/Z9tK++Z79nn2qtBQAAgP58y6QL\nAAAAYGkEOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiUQAcAANApgQ4AAKBTAh0AAECnVk+6\ngPlccMEFbd26dZMu46zw8MMP57zzzpt0GTAv/cm00ptMK73JNNOf4/Xxj3/8z1tr37HQclMZ6Nat\nW5c77rhj0mWcFUajUWZmZiZdBsxLfzKt9CbTSm8yzfTneFXV5xeznCGXAAAAnRLoAAAAOiXQAQAA\ndEqgAwAA6JRABwAA0CmBDgAAoFMCHQAAQKcEOgCAKXfgwIFccsklueyyy3LJJZfkwIEDky4JmBJT\n+cXiAADMOnDgQHbu3Jn9+/fn+PHjWbVqVbZs2ZIk2bx584SrAybNGToAgCm2a9eu7N+/P5s2bcrq\n1auzadOm7N+/P7t27Zp0acAUEOgAAKbYkSNHcumllz5h2qWXXpojR45MqCJgmgh0AABTbP369bn9\n9tufMO3222/P+vXrJ1QRME0EOgCAKbZz585s2bIlhw4dymOPPZZDhw5ly5Yt2blz56RLA6aAi6IA\nAEyxExc+2b59e44cOZL169dn165dLogCJBHoAACm3ubNm7N58+aMRqPMzMxMuhxgihhyCQAA0CmB\nDgAAoFMCHQAAQKcEOgAAgE4JdAAAAJ1aMNBV1UVVdaiq7q6qT1XVzw3Tn1tVt1bVZ4afzznF898y\nLPOZqnrLuF8AAADASrWYM3SPJfmF1tqGJK9I8taq2pBkR5LbWmsvSnLb8PgJquq5Sd6R5AeTvDzJ\nO04V/AAAAHh6Fgx0rbX7W2t3DvcfSnIkyYVJ3pjkhmGxG5L82DxP/5Ekt7bWvtxa+0qSW5O8bhyF\nAwAArHRP64vFq2pdku9L8odJ1rbW7h9m/VmStfM85cIkX5jz+N5h2nzr3ppka5KsXbs2o9Ho6ZTG\nKRw9etS+ZGrpT6aV3mRa6U2mmf6cjEUHuqp6ZpL3J3lba+2rVfX4vNZaq6q2nEJaa/uS7EuSjRs3\ntpmZmeWsjsFoNIp9ybTSn0wrvcm00ptMM/05GYu6ymVVnZPZMPfe1trvDJO/VFXPH+Y/P8kD8zz1\nviQXzXn8wmEaAAAAy7SYq1xWkv1JjrTWrpkz6wNJTly18i1Jfm+ep38oyWur6jnDxVBeO0wDAABg\nmRZzhu6VSX4yyauq6q7hdnmS3UleU1WfSfLq4XGqamNV/WaStNa+nORXk3xsuP3KMA0AAIBlWvAz\ndK2125PUKWZfNs/ydyT5h3MeX5/k+qUWCAAAwPwW9Rk6AAAApo9ABwAA0CmBDgAAoFMCHQAAQKcE\nOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiUQAcAANApgQ4AAKBTAh0AAECnBDoAAIBOCXQA\nAACdEugAAAA6JdABAAB0SqADAADolEAHAADQKYEOAACgUwIdAABApwQ6AACATgl0AAAAnRLoAAAA\nOiXQAQAAdGr1QgtU1fVJ3pDkgdbaJcO0307y4mGRZyf5i9bay+Z57j1JHkpyPMljrbWNY6obAABg\nxVsw0CV5d5J3JnnPiQmttb934n5V/VqSB5/i+Ztaa3++1AIBAACY34KBrrX24apaN9+8qqokP57k\nVeMtCwAAgIVUa23hhWYD3QdPDLmcM/1/SnLNqYZSVtV/T/KVJC3Ju1pr+55iG1uTbE2StWvX/sD7\n3ve+Rb4EnsrRo0fzzGc+c9JlwLz0J9NKbzKt9CbTTH+O16ZNmz6+mI+sLWbI5VPZnOTAU8y/tLV2\nX1U9L8mtVfXp1tqH51twCHv7kmTjxo1tZmZmmaWRJKPRKPYl00p/Mq30JtNKbzLN9OdkLPkql1W1\nOsnfTfLbp1qmtXbf8POBJDcmeflStwcAAMATLedrC16d5NOttXvnm1lV51XV+SfuJ3ltksPL2B4A\nAABzLBjoqupAko8keXFV3VtVW4ZZb85Jwy2r6gVVddPwcG2S26vqE0n+KMnB1trN4ysdAABgZVvM\nVS43n2L6T88z7YtJLh/ufy7JS5dZHwAAAKew3IuiACvE7LeU9GExV+8FADgbLOczdMAK0lob++3i\nqz54WtYLALBSCHQAAACdEugAAAA6JdABAAB0SqADAADolEAHAADQKYEOAACgUwIdAABApwQ6AACA\nTgl0AAAAnRLoAAAAOiXQAQAAdEqgAwAA6JRABwAA0CmBDgAAoFMCHQAAQKcEOgAAgE4JdAAAAJ0S\n6AAAADol0AEAAHRKoAMAAOiUQAcAANCpBQNdVV1fVQ9U1eE50/5ZVd1XVXcNt8tP8dzXVdV/q6rP\nVtWOcRYOAACw0i3mDN27k7xunun/Z2vtZcPtppNnVtWqJL+R5EeTbEiyuao2LKdYAAAAvmnBQNda\n+3CSLy9h3S9P8tnW2udaa/9fkvcleeMS1gMAAMA8Vi/juT9bVT+V5I4kv9Ba+8pJ8y9M8oU5j+9N\n8oOnWllVbU2yNUnWrl2b0Wi0jNI44ejRo/YlU01/Mo0cOxmXTZs2TbqERTl06NCkS+As4Ng5GUsN\ndP8mya8macPPX0vyM8sppLW2L8m+JNm4cWObmZlZzuoYjEaj2JdMrZsP6k+mkmMn49JaG+v61u04\nmHt2v36s64RxceycjCVd5bK19qXW2vHW2jeSXJfZ4ZUnuy/JRXMev3CYBgAAwBgsKdBV1fPnPPw7\nSQ7Ps9jHkryoqv5KVX1rkjcn+cBStgcAAMCTLTjksqoOJJlJckFV3ZvkHUlmquplmR1yeU+SfzQs\n+4Ikv9lau7y19lhV/WySDyVZleT61tqnTsurAAAAWIEWDHSttc3zTN5/imW/mOTyOY9vSvKkrzQA\nAABg+ZY05BIAAIDJE+gAAAA6JdABAAB0SqADAADolEAHAADQKYEOAACgUwIdAABApxb8HjoAAODs\nUlWTLmHRWmuTLmGqOUMHAAArTGtt7LeLr/rgaVkvT02gAwAA6JRABwAA0CmBDgAAoFMCHQAAQKcE\nOgAAgE4JdAAAAJ0S6AAAADol0AEAAHRKoAMAAOiUQAcAANApgQ4AAKBTAh0AAECnBDoAAIBOCXQA\nAACdEugAAAA6tWCgq6rrq+qBqjo8Z9q/rKpPV9UfV9WNVfXsUzz3nqr6ZFXdVVV3jLNwAACAlW4x\nZ+jeneR1J027NcklrbXvTfInSX7xKZ6/qbX2stbaxqWVCAAAwHwWDHSttQ8n+fJJ025prT02PPxo\nkheehtoAAAB4CqvHsI6fSfLbp5jXktxSVS3Ju1pr+061kqrammRrkqxduzaj0WgMpXH06FH7kqmm\nP5lGjp1MM73JNNOfZ96yAl1V7UzyWJL3nmKRS1tr91XV85LcWlWfHs74PckQ9vYlycaNG9vMzMxy\nSmMwGo1iXzK1bj6oP5lKjp1MLcdNppn+nIglX+Wyqn46yRuS/P3WWptvmdbafcPPB5LcmOTlS90e\nAAAAT7SkQFdVr0vyT5P87dba106xzHlVdf6J+0lem+TwfMsyftu3b8+5556bTZs25dxzz8327dsn\nXRIAADBmCw65rKoDSWaSXFBV9yZ5R2avarkms8Mok+SjrbVtVfWCJL/ZWrs8ydokNw7zVyf59621\nm0/Lq+AJtm/fnr1792bPnj3ZsGFD7r777lx11VVJkmuvvXbC1QEAAOOyYKBrrW2eZ/L+Uyz7xSSX\nD/c/l+Sly6qOJbnuuuu
"text/plain": [
"<matplotlib.figure.Figure at 0x7fa77b174630>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
2018-04-10 11:22:39 +00:00
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"Physique\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
]
},
{
"cell_type": "markdown",
"metadata": {
"slideshow": {
"slide_type": "slide"
}
},
"source": [
"## Techno"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
2018-04-12 18:06:58 +00:00
"execution_count": 48,
"metadata": {
"slideshow": {
"slide_type": "fragment"
}
},
2018-04-10 11:22:39 +00:00
"outputs": [
{
"data": {
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.axes._subplots.AxesSubplot at 0x7fa77b090da0>"
2018-04-10 11:22:39 +00:00
]
},
2018-04-12 18:06:58 +00:00
"execution_count": 48,
2018-04-10 11:22:39 +00:00
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
2018-04-12 18:06:58 +00:00
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA3QAAAEyCAYAAACyDpLjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHjJJREFUeJzt3X+UnXddJ/D3xyZoLd1CrYyFYqNY2XSDRXa2gMbdiYVa\nWhR02ZWsPwDjibrCyh50icZjF90cq3v8edgVo+lSVsxyVIocUktrzYhRQUttIWXAAlukpVKxWBrs\nSlO/+8c8kel0pjOZeyf3PnNfr3PumXuf5/s8zyf3fnLnvuf5cau1FgAAAPrnC0ZdAAAAAGsj0AEA\nAPSUQAcAANBTAh0AAEBPCXQAAAA9JdABAAD0lEAHAADQUwIdAABATwl0AAAAPbVp1AUs5Zxzzmlb\ntmwZdRkbwmc/+9mcccYZoy4DlqQ/GVd6k3GlNxln+nO43vve936qtfalK40by0C3ZcuW3HzzzaMu\nY0OYnZ3NzMzMqMuAJelPxpXeZFzpTcaZ/hyuqvrYasY55BIAAKCnBDoAAICeEugAAAB6SqADAADo\nKYEOAACgpwQ6AACAnhLoAAAAekqgAwAYcwcPHsy2bdtyySWXZNu2bTl48OCoSwLGxFh+sTgAAPMO\nHjyYvXv35sCBA3n44Ydz2mmnZdeuXUmSnTt3jrg6YNTsoQMAGGP79u3LgQMHsmPHjmzatCk7duzI\ngQMHsm/fvlGXBowBgQ4AYIzNzc1l+/btj5i2ffv2zM3NjagiYJwIdAAAY2zr1q05cuTII6YdOXIk\nW7duHVFFwDgR6AAAxtjevXuza9euHD58OMePH8/hw4eza9eu7N27d9SlAWPARVEAAMbYiQufvOpV\nr8rc3Fy2bt2affv2uSAKkGQVe+iq6qlVdbiqPlBVt1fVD3XTz66qG6vqju7nE5dZ/mXdmDuq6mXD\n/gcAAGx0O3fuzNGjR3PTTTfl6NGjwhzwT1ZzyOXxJK9prV2Y5DlJfrCqLkyyJ8lNrbULktzUPX6E\nqjo7yZVJnp3k4iRXLhf8AAAAODkrBrrW2j2ttVu6+w8kmUvylCQvSnJNN+yaJC9eYvFvSnJja+2+\n1tqnk9yY5LJhFA4AADDpTuocuqrakuRrk7wnyVRr7Z5u1l8nmVpikack+fiCx3d105Za9+4ku5Nk\namoqs7OzJ1Mayzh27JjnkrGlPxlXepNxpTcZZ/pzNFYd6Krq8Ul+J8mrW2ufqap/mtdaa1XVBimk\ntbY/yf4kmZ6ebjMzM4Osjs7s7Gw8l4wr/cm40puMK73JONOfo7Gqry2oqs2ZD3Nvbq29tZv8yao6\nt5t/bpJ7l1j07iRPXfD4vG4aAAAAA1rNVS4ryYEkc621n18w6+1JTly18mVJfneJxd+Z5NKqemJ3\nMZRLu2kAAAAMaDV76L4+yXcl+caqurW7XZ7kqiTPr6o7kjyve5yqmq6qX0+S1tp9SX4qyZ93t5/s\npgEAADCgFc+ha60dSVLLzL5kifE3J/neBY+vTnL1WgsEAABgaas6hw4AAIDxI9ABAAD0lEAHAADQ\nUwIdAABATwl0AAAAPSXQAQAA9JRABwAA0FMCHQAAQE8JdAAAAD0l0AEAAPSUQAcAANBTAh0AAEBP\nCXQAAAA9JdABAAD01KZRFwAAsFFV1ahLWJXW2qhLANbIHjoAgHXSWhvq7fzXvmPo6xTmoN8EOgAA\ngJ4S6AAAAHpKoAMAAOgpgQ4AAKCnBDoAAICeEugAAAB6SqADAADoKYEOAACgpzatNKCqrk7ywiT3\ntta2ddPekuTp3ZAnJPm71tozl1j2ziQPJHk4yfHW2vSQ6gYAAJh4Kwa6JG9M8vokbzoxobX27Sfu\nV9XPJbn/MZbf0Vr71FoLBAAAYGkrBrrW2ruqastS86qqkvz7JN843LIAAABYyWr20D2Wb0jyydba\nHcvMb0luqKqW5Fdba/uXW1FV7U6yO0mmpqYyOzs7YGkkybFjxzyXjC39ybjSm4wzvcm48t45GoMG\nup1JDj7G/O2ttbur6klJbqyqD7bW3rXUwC7s7U+S6enpNjMzM2BpJPNv+p5LxpX+ZFzpTcbW9Yf0\nJmPLe+dorPkql1W1Kcm3JXnLcmNaa3d3P+9Ncm2Si9e6PQAAAB5pkK8teF6SD7bW7lpqZlWdUVVn\nnrif5NIkRwfYHgAAAAusGOiq6mCSP03y9Kq6q6p2dbNemkWHW1bVk6vquu7hVJIjVXVbkj9Lcqi1\ndv3wSgcAAJhsq7nK5c5lpr98iWmfSHJ5d/+jSS4asD4AAACWMcghlwAAAIyQQAcAANBTAh0AAEBP\nCXQAAAA9JdABAAD0lEAHAADQUwIdAABATwl0AAAAPSXQAQAA9JRABwAA0FMCHQAAQE8JdAAAAD0l\n0AEAAPSUQAcAANBTAh0AAEBPCXQAAAA9JdABAAD0lEAHAADQUwIdAABATwl0AAAAPSXQAQAA9JRA\nBwAA0FMCHQAAQE8JdAAAAD0l0AEAAPTUioGuqq6uqnur6uiCaf+1qu6uqlu72+XLLHtZVX2oqj5c\nVXuGWTgAAMCkW80eujcmuWyJ6b/QWntmd7tu8cyqOi3J/0jygiQXJtlZVRcOUiwAAACft2Kga629\nK8l9a1j3xUk+3Fr7aGvtc0n+T5IXrWE9AAAALGHTAMu+sqq+O8nNSV7TWvv0ovlPSfLxBY/vSvLs\n5VZWVbuT7E6SqampzM7ODlAaJxw7dsxzydjSn4wrvck405uMK++do7HWQPcrSX4qSet+/lyS7xmk\nkNba/iT7k2R6errNzMwMsjo6s7Oz8VwyrvQn40pvMrauP6Q3GVveO0djTVe5bK19srX2cGvtH5P8\nWuYPr1zs7iRPXfD4vG4aAAAAQ7CmQFdV5y54+K1Jji4x7M+TXFBVX1FVj0vy0iRvX8v2AAAAeLQV\nD7msqoNJZpKcU1V3JbkyyUxVPTPzh1zemeT7urFPTvLrrbXLW2vHq+qVSd6Z5LQkV7fWbl+XfwUA\nAMAEWjHQtdZ2LjH5wDJjP5Hk8gWPr0vyqK80AAAAYHBrOuQSAACA0RPoAAAAekqgAwAA6CmBDgAA\noKcEOgAAgJ4S6AAAAHpKoAMAAOipFb+HDgAA2FiqatQlrFprbdQljDV76AAAYMK01oZ+O/+171iX\n9fLYBDoAAICeEugAAAB6SqADAADoKYEOAACgpwQ6AACAnhLoAAAAekqgAwAA6CmBDgAAoKcEOgAA\ngJ4S6AAAAHpKoAMAAOgpgQ4AAKCnNo26AKAfqmrUJaxaa23UJXAK6U0AJpk9dMCqtNaGfjv/te9Y\nl/UyWfQmAJNMoAMAAOipFQNdVV1dVfdW1dEF0/57VX2wqt5XVddW1ROWWfbOqnp/Vd1aVTcPs3AA\nAIBJt5o9dG9MctmiaTcm2dZa+5okf5nkRx9j+R2ttWe21qbXViIAAABLWTHQtdbeleS+RdNuaK0d\n7x6+O8l561AbAAAAj2EYV7n8niRvWWZeS3JDVbUkv9pa27/cSqpqd5LdSTI1NZXZ2dkhlMaxY8c8\nl4w1/cm40puMK73JONOfp95Aga6q9iY5nuTNywzZ3lq7u6qelOTGqvpgt8fvUbqwtz9Jpqen28zM\nzCCl0ZmdnY3nkrF1/SH9yXjSm4wrvck4058jsearXFbVy5O8MMl3tGWuxdxau7v7eW+Sa5NcvNbt\nAQAA8EhrCnRVdVmS/5LkW1prf7/MmDOq6swT95NcmuToUmMBAAA4eav52oKDSf40ydOr6q6q2pXk\n9UnOzPxhlLdW1Ru6sU+uquu6RaeSHKmq25L8WZJDrbXr1+VfwaMcPHgw27ZtyyWXXJJt27bl4MGD\noy4JAAAYshXPoWut7Vxi8oFlxn4iyeXd/Y8muWig6liTgwcPZu/evTlw4EAefvjhnHbaadm1a1eS\nZOfOpV5OAACgj9Z8Dh3ja9++fTlw4EB27NiRTZs2ZceOHTlw4ED27ds36tIAAIAhGsbXFjBm5ubm\nsn379kdM2759e+bm5kZ
2018-04-10 11:22:39 +00:00
"text/plain": [
2018-04-12 18:06:58 +00:00
"<matplotlib.figure.Figure at 0x7fa77b0ae940>"
2018-04-10 11:22:39 +00:00
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
2018-04-12 18:06:58 +00:00
"df[[\"Techno\", \"Classe\"]].set_index(\"Classe\", append=True).unstack(1).boxplot(figsize=(15, 5))"
2018-04-10 11:22:39 +00:00
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true
},
"outputs": [],
"source": []
}
],
"metadata": {
2018-04-12 18:06:58 +00:00
"celltoolbar": "Slideshow",
2018-04-10 11:22:39 +00:00
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}