lafrite/FAOD-DUI5
1
0
Fork 0
Code Issues Pull Requests Releases Wiki Activity
3999715dc7
FAOD-DUI5/FOAD-bloc5.md

14 KiB
Raw Blame History

Recherche du plus grand carré blanc dans une "image"

Objectif et déroulement

On considère le problème suivant : étant donné une image monochrome n \times n, déterminer le plus grand carré qui ne contient aucun point noir.

Le but du TP est d'établir plusieurs algorithmes permettant de trouver le plus grand carré blanc dans une image.

Déroulement du TP :

  • Conception d'un algorithme récursif naïf : RechercheCarreBlanc_naif()
  • Programmation dynamique - Utilisation de la mémoïsation : RechercheCarreBlanc_memoisation()
  • Programmation dynamique - Optimisation par "Bottom_up" : RechercheCarreBlanc_BU()

Conception d'un algorithme récursif naïf : RechercheCarreBlanc_naif()

Une image c'est quoi ?

Une image, c'est un tableau de tuples qui représentent les couleurs des pixels. Dans le cadre de ce TP, nous nous limiterons à des images noir et blanc :

Image N/B

t=[
    [1,0,0,1,0,0,1,0,0,1],
    [0,0,0,0,0,0,1,0,0,0],
    ...
    [0,0,0,0,1,0,0,0,1,0]
]

t[5][1]==1 car le pixel de la ligne 5 et de la colonne 1 est noir. (Attention les numéros des lignes/colonnes commencent à 0).

Etude du problème

L'objectif est de trouver le carré blanc le plus grand possible à partir d'un pixel donné (coin inférieur droit).

  • PlusGrandCarreBlanc_Rec(lig,col) : Retourne la taille du carré blanc à partir du coin inférieur droit (ligne,colonne).

Par ex :

  • PlusGrandCarreBlanc_Rec(1,2) == 2
  • PlusGrandCarreBlanc_Rec(6,4) == 2

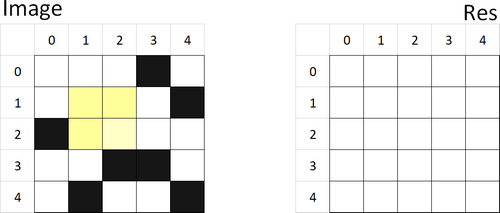
Image N/B

  1. Pour l'image suivante, donner le résultat de :
  • PlusGrandCarreBlanc_Rec(2,1) == ...
  • PlusGrandCarreBlanc_Rec(1,2) == ...
  • PlusGrandCarreBlanc_Rec(1,1) == ...

Image N/B

  1. Quelle relation existe-il entre PlusGrandCarreBlanc_Rec(2,2) et les 3 valeurs précédentes ?

  2. Généraliser ce résultat pour un pixel quelconque :

PlusGrandCarreBlanc_Rec(lig,col) = min( ......... , ......... , ......... ) + .........

  1. Proposer un algorithme récursif pour PlusGrandCarreBlanc_Rec(i,j) :
def PlusGrandCarreBlanc_Rec(t,lig,col):     # t est le tableau représentant l'image noir et blanc

    if t(lig, col) == 1:                    # Si le pixel est noir
        return ...                          # On retourne ... 

                                            # Sinon :
    elif ...... :                           # Si le pixel est sur la 1ère ligne ou 1ère colonne
        return ...                          # On retourne ...

    else :                                  # Sinon :
        return ...                          # On retourne 1 + min(PlusGrandCarre des pixels adjacents)
                                            # Adjacents => à gauche, en haut, en diagonale haut-gauche
  1. Tester votre algorithme sur le tableau suivant :
t=[ [0,0,0,1,0],
    [0,0,0,0,1],
    [1,0,0,0,0],
    [0,0,1,1,0],
    [0,1,0,0,1] ]

>>> print(PlusGrandCarreBlanc_Rec(t,2,2))
2

Remarque : D'autres tableaux sont présent dans le fichier TP.py

Remarque : Lors de l'évaluation du minimum par min(), l'interpréteur DOIT calculer les 3 valeurs à comparer. Or, nous pouvons lui éviter dans certains cas ce travail (et économiser un nombre d'appels récursifs). En effet, si la première valeur calculée est nulle alors le min(... , ... , ...) retournera FORCEMENT 0 et la fonction retournera 1. De même pour la seconde et la troisième.

  1. Modifier PlusGrandCarreBlanc_Rec(lig,col) en tenant compte de la remarque précédente.
def PlusGrandCarreBlanc_Rec(t,lig,col):
    ...
    else :                                  
        g = ...                   # Valeur du pixel de gauche
        if g==0:
              return 1
        h = ...                   # Valeur du pixel du haut
        if h==0:
              return 1
        ...                       # ...
        return ...                # On retourne 1 + min(g,h,...)
  1. Ecrire un algorithme simple pour afficher t à l'aide de matplotlib et vérifier le bon fonctionnement de votre algorithme.

Aide

import matplotlib.pyplot as plt
...
plt.imshow(t,cmap='binary')
plt.show()

  1. Ecrire un algorithme qui parcourt toute l'image et qui retourne la ligne et la colonne du carré le plus grand ainsi que sa taille.

    • RechercheCarreBlanc_naif(t) : Retourne la ligne et la colonne du coin inférieur droit du carré blanc le plus grand ainsi que sa taille.
def RechercheCarreBlanc_naif(t):
    ...
    for lig in range(...):
        for col in range(...):
            ...
    return l,c,tmax

  1. Bonus : Faire en sorte d'afficher ce carré lors de l'affichage de l'image.

  2. Ajouter un compteur (variable global) compteur_naif permetttant de compter le nombre d'appels récursifs

  3. Ecrire une fonction permettant de générer un tableau de n\times n content un ratio de points noir de ratio_noir%

def genere_tab_alea(n, ratio_noir):
    ...
    return t

Programmation dynamique - Utilisation de la mémoïsation : RechercheCarreBlanc_memoisation()

Remplacons nous dans le cadre d'un cas simple, on cherche PlusGrandCarreBlanc_Rec(2,2).

Image N/B

  1. Pendant l'appel de PlusGrandCarreBlanc_Rec(2,2), quelles sont les 3 appels récursifs qui vont être exécutés ?
  • Appel n°1 : PlusGrandCarreBlanc_Rec( ... , ... )
  • Appel n°2 : PlusGrandCarreBlanc_Rec( ... , ... )
  • Appel n°3 : PlusGrandCarreBlanc_Rec( ... , ... )
  1. Compléter le tableau suivant qui liste, pour les appels n°1, n°2 et n°3, les appels récursifs exécutés.
Appel n°1 : PGCB_Rec( ... , ... ) Appel n°2 : PGCB_Rec( ... , ... ) Appel n°3 : PGCB_Rec( ... , ... )
PGCB_Rec( ... , ... ) PGrCB_Rec( ... , ... ) PGCB_Rec( ... , ... )
PGCB_Rec( ... , ... ) PGrCB_Rec( ... , ... ) PGCB_Rec( ... , ... )
PGCB_Rec( ... , ... ) PGrCB_Rec( ... , ... ) PGCB_Rec( ... , ... )
  1. Quels appels sont redondants ? Proposez une solution pour éviter cela.

Mise en place du tableau de mémoïsation

Pour économiser des appels récursifs, vous allez stocker au fur et à mesure les résultats de ces appels dans un tableau de même taille que l'image.

Ce tableau sera initialisé entièrement à -1, ce qui signifie qu'aucun résultat n'a déjà été calculé pour ce pixel. Dans le cas contraire, il faudra stocker le résultat dans ce t_memo

  • t_memo : Tableau de même dimension que t qui stocke les valeurs de PlusGrandCarreBlanc_memo() au fur et à mesure des appels récursifs. Ce tableau est une variable globale.
  1. Initialiser la variable globale t_memo.

Aide : En une ligne ... t_memo = [[-1 for i in ... ] for j ... ]

Remarque : On peut être malin et faire une copie de t en remplaceant les 1 (pixel noir) par des 0 (résultat connu) et les 0 (pixels blancs) par des -1 (résultat inconnu)

Évolution de PlusGrandCarreBlanc_Rec() en PlusGrandCarreBlanc_memo()

  1. En vous aidant de PlusGrandCarreBlanc_Rec(), écrire la fonction PlusGrandCarreBlanc_memo() en stockant et utilisant les résultats précédamment calculés dans le tableau t_memo
def PlusGrandCarreBlanc_memo(t, lig, col):
    if t_memo[lig][col] != -1:          # Utilisation d'une valeur présente dans t_memo
        return ...
    if t[lig][col] == 1:
    ...
    return ...
  1. Effectuer les tests sur différents pixels d'une image et sur différentes images. Vous pouvez aussi utiliser la fonction genere_tab_alea(n, ratio_noir) pour valider votre algorithme.

Pour aller plus vite ... RechercheCarreBlanc_memo() ?

PlusGrandCarreBlanc_memo() est une fonction équivalente à PlusGrandCarreBlanc_Rec() mais normalement plus rapide.

Il reste donc à parcourir une image pour trouver les coordonnées du coin inférieur droit du plus grand carré blanc dans l'image.

  1. Ecrire la fonction RechercheCarreBlanc_memo() qui retourne les coordonnées du coin inférieur droit du plus grand carré blanc ainsi que sa taille.
def RechercheCarreBlanc_memo(t):
    l, c, tmax = 0, 0, 0
    ...
    return l, c, tmax

Complexité

  1. A l'aide du module time, mesurer la différence de performance de l'algorithme naïf et de celui qui utilisa le mémoïsation sur des images de tailles et de "ratio de noir" différents.
~ n=10 / ratio=50 n=30 / ratio=50 n=50 / ratio=40 n=70 / ratio=35
RechercheCarreBlanc_Rec ~ ~ ~ ~
RechercheCarreBlanc_memo ~ ~ ~ ~
  1. De la même manière que pour l'algorithme naïf, implanter un compteur_memo qui permettra de compter le nombre d'appels récursifs. Effectuer les tests avec les mêmes paramètres que dans la question précédente.
~ n=10 / ratio=50 n=30 / ratio=50 n=50 / ratio=40 n=70 / ratio=35
RechercheCarreBlanc_Rec ~ ~ ~ ~
RechercheCarreBlanc_memo ~ ~ ~ ~

Uniquement avec RechercheCarreBlanc_memo, mesurer le temps d'exécution de l'algorithme avec n=500 / ratio=50 puis avec n=1000 / ratio=50.

  1. Par combien a été multiplié le temps d'exécution lorsque n a doublé ? Conjecturer sur la complexité de cet algorithme.

  2. Le gain de performance est-il subtanciel ?

Roadrunner

Programmation dynamique - Optimisation "Bottom Up" : RechercheCarreBlanc_BU()

L'optimisation "BOTTOM UP", consiste à traiter les problèmes du plus évident (les "plus petits") au moins évident (les "plus gros") en stockant les résultats au fur et à mesure dans un tableau.

Il faut toutefois identifier un ordre dans lequel résoudre les sous-problèmes. Dans notre cas l'ordre est :

  • Traiter les problèmes de taille "0" : Les cases noires
  • Traiter les problèmes de taille "1" : Les cases sur la première ligne et première colonne
  • Traiter les problèmes de taille "2" : ...

Le tableau de "résultats", qui stocke au fur et à mesure les résultats de PlusGrandCarreBlanc(lig,col), se nommera res.

  1. Compléter, à la main, le tableau res pour les problèmes de taille "0".
  • Si le pixel(lig,col) est noir alors res[lig][col] = 0

Image N/B

  1. Compléter, à la main, le précédent tableau res pour les problèmes de taille "1".
  • Si le pixel(lig,col) est sur la première ligne et/ou colonne alors res[lig][col] = 1

Image N/B

  1. En l'état actuel, peut-on, à l'aide de res, calculer PlusGrandCarreBlanc(1,1) directement (sans calcul intermédiaire) ? et PlusGrandCarreBlanc(2,2) ?

  2. Comment faut-il parcourir le tableau pour être sûr qu'à chaque appel, l'algorithme dispose des résultats des problèmes de taille inférieur.

  3. Ecrire un algorithme PlusGrandCarreBlanc_BU() qui :

  • Initialise le tableau res à -1
  • Complète res avec les résultats de taille "0" (les cases noires)
  • Complète res avec les résultats de taille "1" (1ère ligne/colonne)
  • Parcours l'image et calcule les résultats de taille supérieur
  • Et retourne res

Aide :

  • Remplir un tableau res, qui a la même taille que l'image, et qui est initialisé -1 dans toutes les cases.
  • A l'aide de 2 boucles imbriquées sur les lignes et colonnes :
    • Si le t[lig][col] est noir, affectez 0 à res[lig][col]
    • Sinon si lig==0 ou col==0, affectez 1 à res[lig][col]
      • Sinon affectez min(res[lig][col-1] , res[lig-1][col-1] , res[lig-1][col] ) + 1 à res[lig][col]
  • Retourner res
def PlusGrandCarreBlanc_BU(t):
    nb_lig, nb_col = ...
    res = [[-1 for i in ...] for j in ...]
    for lig in range(nb_lig):
        for col in range(nb_col):
            ...
    return res

.... et trouver le carré blanc le plus grand (presque à la vitesse de la lumière) : RechercheCarreBlanc_BU()

  1. Ecrire RechercheCarreBlanc_BU() qui retourne les coordonnées du coin inférieur droit du plus grand carré blanc ainsi que sa taille à l'aide de l'algorithme précédent.
def RechercheCarreBlanc_BU(t):
    l, c, tmax = 0, 0, 0
    ...
    return l, c, tmax

Comparaison des algorithmes

  1. Comparer le temps d'éxecution des ces algorithmes.
~ n=100 / ratio=30 n=300 / ratio=20 n=1000 / ratio=20 n=3000 / ratio=40
RechercheCarreBlanc_memo ~ ~ ~ ~
RechercheCarreBlanc_BU ~ ~ ~ ~

Conclusion

Programmation dynamique = Gain en performance

L'étude théorique d'un problème permet une optimisation précise de l'algorithme qui le résoudra.

Programmation dynamique